Problème de la hauteur d'étoile
Le problème de la hauteur d'étoile, en théorie des langages formels, est le problème qui consiste à déterminer la hauteur d'étoile d'un langage rationnel, c'est-à-dire le nombre minimal d'étoiles de Kleene imbriquées nécessaires dans une expression rationnelle pour qu'elle puisse dénoter ce langage. Il existe des langages rationnels de hauteur d'étoile arbitrairement grande, mais la détermination de la hauteur d'étoile d'un langage rationnel, tout en étant décidable, est très difficile.
Définition de la hauteur d'étoile
Hauteur d'étoile d'une expression rationnelle

La hauteur d'étoile d'une expression rationnelle est le nombre maximum d'étoiles emboîtées nécessaires pour la décrire. Par exemple, la hauteur d'étoile de l'expression rationnelle est égale à . Toutefois, la hauteur d'étoile d'une expression rationnelle n'est pas nécessairement le nombre d'étoile apparaissant dans l'expression. Par exemple, la hauteur d'étoile de l'expression rationnelle est égale à alors que le nombre d'étoiles est .
Plus formellement, on définit la hauteur d'étoile d'une expression rationnelle comme étant le nombre défini récursivement comme suit :
- pour toute lettre
- .
Hauteur d'étoile d'un langage rationnel
On souhaite étendre cette définition aux langages rationnels. Cependant, il est à noter que deux expressions rationnelles différentes peuvent avoir une hauteur d'étoile différente tout en décrivant le même langage. Par exemple, on a : mais . On ne peut donc pas définir la hauteur d'étoile d'un langage rationnel comme étant la hauteur d'étoile d'une expression rationnelle arbitraire le décrivant. C'est pourquoi la hauteur d'étoile d'un langage rationnel est défini comme étant le minimum des hauteurs d'étoile des expressions dénotant ce langage, c'est-à-dire :
.
On peut, par exemple, se servir de cette notion pour caractériser un certain type de langage : un langage rationnel est fini (i.e. ne possède qu'un nombre fini de mots) si et seulement si sa hauteur d'étoile est nulle.
Caractérisation par automates finis
Le problème de la hauteur d'étoile concerne les langages rationnels, il peut être utile d'étudier la manière de le traiter avec des automates finis. Dans ce paragraphe, on s'intéresse au calcul de la hauteur d'étoile d'un langage rationnel décrit par un automate fini.
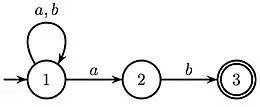
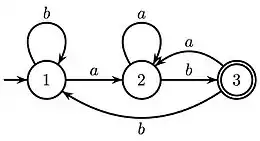
Afin de réaliser ce calcul, on observe qu'une étoile d'une expression rationnelle est représentée par un cycle dans le graphe d'un automate (la notion de cycle pour un automate correspond à celle de circuit dans un graphe). Par extension, on peut remarquer que la notion de hauteur d'étoile pour une expression rationnelle correspond au nombre de cycles imbriqués dans un automate dénotant celle-ci. De la même manière que précédemment, deux automates reconnaissant le même langage peuvent avoir un nombre de cycles imbriqués différent. Par exemple, les automates des Fig .1 et Fig. 2 reconnaissent tous les deux le même langage des mots qui finissent par , mais l'automate 1 possède un cycle imbriqué (autour du sommet 1) tandis que l'automate 2 en a deux (autour du sommet 1 et des sommets 2 et 3).
Rang cyclique d'un automate
La notion de rang cyclique[1] d'un automate[2] permet de justifier plus précisément le lien qu'il y a entre le problème de la hauteur d'étoile d'un langage et le nombre de cycles imbriqués des automates acceptant celui-ci. Les notions s'appliquent à des automates déterministes ou non, et sont en fait des notions de graphes.
On définit la notion de rang pour une composante fortement connexe d'un graphe comme suit. Le rang est égal à :
- 0 si la composante possède un unique sommet n'a pas de boucle autour de ce sommet ;
- 1 s'il existe un sommet par lequel passent tous les cycles de cette composante
- k (avec k ≥ 2) s'il existe un sommet tel que le graphe obtenu en supprimant ce sommet et les arcs qui lui sont adjacents (c'est-à-dire dont ce sommet est l’origine ou la destination) contient un cycle de rang k−1 (et éventuellement des cycles de rang inférieur), et si le graphe obtenu en supprimant tout autre sommet que celui du cycle initial contient au moins un cycle de rang supérieur où égal k-1. En d'autres termes, c'est 1+ le plus petit des rangs obtenus en supprimant un sommet.
Le rang cyclique d'un automate est défini comme suit :
- Si l'automate est acyclique, son rang cyclique est nul (dans ce cas, le langage reconnu est fini) ;
- sinon, il est égal au maximum du rang de ses composantes connexes (qui existent car l'automate possède au moins un cycle).
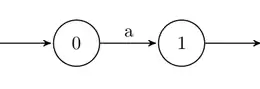
L'automate de la Fig. 3 est de rang cyclique 0 car il est acyclique (le langage qu'il reconnaît est réduit au mot a et est donc fini). Un exemple d'automate de rang cyclique 1 est celui de la Fig. 1 car tous les cycles de celui-ci passent par le sommet 1. Enfin, l'automate représenté sur la Fig. 2 est, lui, de rang cyclique 2 : si on supprime l’un des sommets, le graphe résultant est de rang 1.
Théorèmes liant rang cyclique et hauteur d'étoile
L'utilisation du rang cyclique d'un automate se justifie ici grâce au théorème suivant qui exprime la hauteur d'étoile d'un langage en fonction du rang cyclique des automates qui le reconnaissent.
Théorème (Eggan, 1963) — La hauteur d’étoile d’un langage rationnel est égal au minimum des rangs cycliques des automates finis reconnaissant ce langage.
Le théorème de Eggan[3] démontre donc qu'en connaissant tous les automates finis d'un langage, on est capable d'en déduire sa hauteur d'étoile. Cependant, comme existe plusieurs automates finis reconnaissant un même langage, le minimum à calculer dans le théorème impose que l’on ne peut pas utiliser seulement un automate particulier. De plus, la hauteur d'étoile n'est pas une propriété syntaxique (sinon un langage et son complément auraient la même hauteur, ce qui n'est pas le cas : il suffit de prendre le langage de tous les mots et son complémentaire, le langage vide), et donc on ne peut pas se contenter d'étudier son automate minimal. Toutefois, et sous certaines conditions, on peut quand même utiliser un automate minimal. Cela fait l'objet du théorème[4] suivant :
Théorème (McNaughton, 1967) — Soit un langage rationnel. Si le monoïde syntactique de est un groupe et si l’automate minimal de possède un seul état final, alors la hauteur d’étoile du langage est égale au rang cyclique de cet automate.
- Exemple
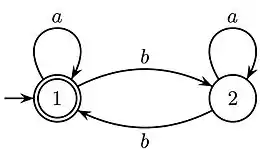
Soit l'ensemble des mots sur l'alphabet qui contiennent un nombre pair de . L'automate déterministe minimal reconnaissant est donné dans la figure ci-contre. Les lettres réalisent des permutations des états de l’automate, donc le monoïde syntaxique est un groupe. Par le théorème, on en déduit que la hauteur d'étoile de est égal au rang cyclique de cet automate, ici 2. Un expression régulière pour le langage est .
Ces théorèmes montrent que le problème de la hauteur d'étoile peut se réduire à un problème de complexité dans un automate reflété par le nombre de circuits imbriqués. Cette réduction du problème sur un langage à un problème sur les automates s'avère très utile pour montre la décidabilité du problème de la hauteur d'étoile d'un langage.
Des langages de hauteur d'étoile arbitrairement grande
Le problème de savoir s'il existe des langages rationnels de hauteur d'étoile arbitrairement grande a été posé par L. C. Eggan[3] en 1963. La réponse à cette question se décline sous plusieurs formes.
La solution d'Eggan
Une première réponse a été donnée par Eggan lui-même. Les premiers des langages donnés par Eggan[3] sont décrits par les expressions rationnelles suivantes :
Le principe de construction de ces expressions est le suivant : l’expression est obtenue en concaténant deux copies de , où les lettres de la deuxième sont renommées par des symboles nouveau, le tout entouré d'une étoile de Kleene. Par construction, la hauteur de l'expression est n. Pour montrer que le langage dénoté par cette expression est aussi n, il reste la partie difficile à prouver, à savoir qu'il n'existe pas d'expression rationnelle de hauteur d'étoile plus petite que n décrivant le même langage que celui décrit par . Une démonstration est donnée dans l'article de Eggan[3].
On peut donner une autre construction permettant de montrer que la hauteur d'étoile d'un langage n'est pas bornée. On utilise pour cela le théorème de McNaughton (vu plus haut). Pour tout n de N, on considère un langage rationnel sur un alphabet de n lettres dont l’automate minimal n’a qu’un seul état final et tel que la lecture de chacune des n lettres est une permutation des états de l’automate. Dans ce cas, le monoïde syntaxique est un groupe. Ainsi, par le théorème de McNaughton, ce langage est de hauteur d’étoile égale à n.
Le défaut des exemples de Eggan est qu'il utilise des langages ayant un nombre de lettres arbitrairement grand pour construire des langages de hauteur d'étoile de plus en plus grande. Il pose lui-même la question de savoir s'il existe des exemples avec un alphabet à deux lettres.
La solution de Dejan et Schützenberger
Une réponse positive a été donnée peu de temps après dans l'article de Dejean et Schützenberger [5]. Leurs exemples sont définis par récurrence. La famille d'expressions régulières sur l’alphabet binaire est la suivante[6] :
Ainsi :
À nouveau, une preuve rigoureuse est nécessaire pour démontrer que pour l'expression il n'y a pas d'expression de hauteur d'étoile plus petite. On trouve les preuves dans l'article original[5] et dans l'ouvrage de Salomaa[6].
Décidabilité de la hauteur d'étoile d'un langage
Le problème de déterminer la hauteur d'étoile d'un langage est de trouver une expression de la plus petite hauteur pour un langage donnée. Le problème est devenue un problème ouvert célèbre en théorie des langages formels, comme l'écrit Brzozowski en 1980[7]. Les langages purs à groupe (en) constituent la première famille de langages rationnels pour laquelle il a été démontré que le problème de la hauteur d'étoile est décidable[4]. Le problème général a été résolu par Kosaburo Hashiguchi (en) en 1988[8] :
Théorème (Hashigushi, 1988) — La hauteur d’étoile d’un langage rationnel est décidable.
Hashiguchi a publié un algorithme qui détermine la hauteur d'étoile d'un langage rationnel quelconque. L'algorithme est de complexité non élémentaire. Un algorithme bien plus efficace a été développé par Daniel Kirsten en 2005. La complexité en espace de l'algorithme, pour un automate fini non déterministe, est doublement exponentielle. Une version simplifiée a été proposée en 2015, par Mikolaj Bojanczyk[9]. Sa démonstration commence, comme celle de Kirsten, par une réduction du problème à un problème concernant des automates avec compteurs, appelé « problème de limitation » (en anglais « limitedness problem »). Il présente ensuite un nouvel algorithme pour le problème de limitation en le ramenant à la résolution d'un jeu particulier, le jeu de Gale et Stewart[10], qui possède une stratégie gagnante ω-régulière.
Problème de hauteur d'étoile généralisée
Le problème de hauteur d'étoile généralisée est la question - toujours ouverte en 2016 - de savoir si tout langage rationnel possède une expression régulière généralisée avec une hauteur d'étoile bornée. Dans ce contexte, une expression est généralisée si elle autorise également la complémentation. Les langages de hauteur généralisée 0 sont exactement les langages sans étoile. En particulier, il n'est pas connu si la hauteur d'étoile 1 est suffisante[11].
Articles connexes
- Generalized star height problem (en)
- Algorithme de McNaughton et Yamada
- Algorithme de Conway
- Théorie des jeux
Notes et références
- En anglais « loop complexity »
- L'exposé suit Bassino 1996, section 2.1.2 : Lien avec les automates. Sakarovitch 2009 section I.6 : Sar height en fait une description plus détaillée.
- Eggan 1963.
- McNaughton 1967
- Dejean et Schützenberger 1966
- Salomaa 1981
- Brzozowski 1980
- Hashiguchi 1988
- Bojanczyk 2015
- Gale et Stewart 1953.
- Sakarovitch 2009.
Bibliographie
- Frédérique Bassino, Séries rationnelles et distributions de longueurs (Thèse de doctorat en informatique fondamental), (lire en ligne), p. 63-73
- Lawrence C. Eggan, « Transition graphs and the star-height of regular events », Michigan Mathematical Journal, vol. 10, no 4, , p. 385–397 (DOI 10.1307/mmj/1028998975, zbMATH 0173.01504)
- Françoise Dejean et Marcel-Paul Schützenberger, « On a Question of Eggan », Information and Control, vol. 9, no 1, , p. 23–25 (DOI 10.1016/S0019-9958(66)90083-0)
- Robert McNaughton, « The Loop Complexity of Pure-Group Events », Information and Control, vol. 11, nos 1–2, , p. 167–176 (DOI 10.1016/S0019-9958(67)90481-0)
- Janusz A. Brzozowski, « Open problems about regular languages », dans Ronald V. Book, Formal language theory—Perspectives and open problems, New York, Academic Press, (ISBN 0-12-115350-9, lire en ligne), p. 23–47
- Arto Salomaa, Jewels of Formal Language Theory, Melbourne, Pitman Publishing, (ISBN 0-273-08522-0, zbMATH 0487.68063)
- Kosaburo Hashiguchi, « Regular languages of star height one », Information and Control, vol. 53, no 2, , p. 199–210 (DOI 10.1016/S0019-9958(82)91028-2)
- Kosaburo Hashiguchi, « Algorithms for Determining Relative Star Height and Star Height », Information and Computation, vol. 78, no 2, , p. 124–169 (DOI 10.1016/0890-5401(88)90033-8)
- Sylvain Lombardy et Jacques Sakarovitch, « Star Height of Reversible Languages and Universal Automata », dans 5th Latin American Symposium on Theoretical Informatics (LATIN) 2002, Springer, coll. « Lecture Notes in Computer Science vol. 2286 », (lire en ligne)
- Daniel Kirsten, « Distance Desert Automata and the Star Height Problem », RAIRO - Informatique Théorique et Applications, vol. 39, no 3, , p. 455–509 (DOI 10.1051/ita:2005027)
- (en) Jacques Sakarovitch (trad. Reuben Thomas), Elements of automata theory, Cambridge, Cambridge University Press, , 758 p. (ISBN 978-0-521-84425-3, zbMATH 1188.68177)
- Mikolaj Bojanczyk, « Star Height via Games », 30th Annual ACM\/IEEE Symposium on Logic in Computer Science, Institute of Electrical & Electronics Engineers (IEEE), , p. 214-219 (ISBN 978-1-4799-8875-4, DOI 10.1109/lics.2015.29, lire en ligne).
- David Gale et F. M. Stewart, « Infinite games with perfect information », Annals of Mathematics Studies, Princeton University Press, no 28, , p. 245–266 (MR 0054922)































