Polyèdre fractal

Soit un polyèdre ${\displaystyle P}$ d'ordre n, à n sommets notés ${\displaystyle S_{i}}$. Le polyèdre fractal associé est construit en appliquant itérativement à ce polyèdre un système de n homothéties ${\displaystyle H_{i}}$ sur ${\displaystyle \scriptstyle {\mathbb {R} ^{3}}}$, de rapport unique ${\displaystyle R}$ telles que:

• le centre de l'homothétie ${\displaystyle H_{i}}$ est le sommet ${\displaystyle S_{i}}$.
• le rapport ${\displaystyle R}$ est le plus grand rapport tel que l'intersection de deux quelconques des polyèdres images soit de volume nul.

Le rapport est donc déterminé pour que l'ensemble soit tout juste connexe, les intersections étant limitées à des points ou des arêtes.

On définit à partir des homothéties ${\displaystyle H_{i}}$ une nouvelle fonction ${\displaystyle H}$, elle aussi contractante sur ${\displaystyle \scriptstyle {\mathbb {R} ^{3}}}$ muni de la distance de Hausdorff, par l'expression ${\displaystyle \scriptstyle {H(P)=\bigcup _{i=1}^{n}H_{i}(P)}}$. ${\displaystyle H(P)}$ est un ensemble de n polyèdres similaires à ${\displaystyle P}$.

Le théorème du point fixe assure l'existence et l'unicité d'un sous-ensemble fixe ${\displaystyle F}$ de ${\displaystyle \scriptstyle {\mathbb {R} ^{3}}}$ tel que ${\displaystyle H(F)=F}$. ${\displaystyle F}$ est appelé attracteur du système de fonctions itérées H. En pratique, F est obtenu comme la limite ${\displaystyle H^{n}(F_{0})}$ pour ${\displaystyle n\to \infty }$ où ${\displaystyle F_{0}}$ est un compact quelconque, tel que le polyèdre ${\displaystyle P}$.

Pour chaque polyèdre platonique, à l'exception notable du cube, en itérant à l'infini, l'ensemble résultant est un ensemble fractal. Pour obtenir un ensemble connexe, le rapport d'homothétie nécessaire pour le cube serait 1/2. Mais l'ensemble résultant est le cube lui-même et n'est donc pas fractal.

On appelle polyèdre fractal platonique un polyèdre fractal issu d'un polyèdre régulier convexe. Le cube ne génère pas d'ensemble fractal selon les règles mentionnées ci-dessus.

	Tétraèdre fractal	Octaèdre fractal	Dodécaèdre fractal	Icosaèdre fractal
Nombre d'homothéties	4	6	20	12
Rapport d'homothétie	${\displaystyle \textstyle {{\frac {1}{2}}=0,5}}$	${\displaystyle \textstyle {{\frac {1}{2}}=0,5}}$	${\displaystyle \textstyle {{\frac {1}{2+\varphi }}\approx 0,2763}}$	${\displaystyle \textstyle {{\frac {1}{1+\varphi }}\approx 0,3819}}$
Dimension fractale	${\displaystyle \textstyle {{\frac {\ln(4)}{\ln(2)}}=2}}$	${\displaystyle \textstyle {{\frac {\ln(6)}{\ln(2)}}\approx 2,5849}}$	${\displaystyle \textstyle {{\frac {\ln(20)}{\ln(2+\varphi )}}\approx 2,3296}}$	${\displaystyle \textstyle {{\frac {\ln(12)}{\ln(1+\varphi )}}\approx 2,5819}}$

Tétraèdre fractal ou tétraèdre de Sierpinski

Tétraèdre de Sierpinski après la troisième itération

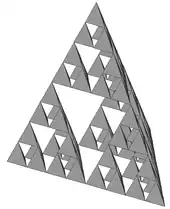
Le tétraèdre fractal est l'extension naturelle à la 3^e dimension du triangle de Sierpinski. Il a la particularité d'avoir pour dimension 2. En conséquence, sa surface ne varie pas d'une itération à l'autre. A l'infini, sa surface est identique à celle du tétraèdre d'origine.

	Volume	Surface
A l'itération n	${\displaystyle {\frac {\sqrt {2}}{3*2^{n+2}}}a^{3}}$	${\displaystyle {\sqrt {3}}a^{2}}$
% variation entre deux itérations	${\displaystyle -50\%}$	${\displaystyle 0\%}$
A l'infini	${\displaystyle Nul}$	${\displaystyle {\sqrt {3}}a^{2}}$

avec ${\displaystyle a}$ = longueur de l'arête du polyèdre d'origine.

Octaèdre fractal

Octaèdre fractal après la troisième itération

L'octaèdre fractal est le polyèdre fractal dont le volume diminue le plus lentement d'une itération à l'autre.

L'intersection de deux polyèdres images voisins est une arête et non un sommet.

Chaque face est un triangle de Sierpinski.

À la limite, sa surface infinie enveloppe un volume nul.

	Volume	Surface
A l'itération n	${\displaystyle {\frac {3^{n-1}{\sqrt {2}}}{2^{2n}}}a^{3}}$	${\displaystyle {\frac {{3^{n}}{\sqrt {3}}}{2^{n-1}}}a^{2}}$
% variation entre deux itérations	${\displaystyle -25\%}$	${\displaystyle +50\%}$
A l'infini	${\displaystyle Nul}$	${\displaystyle \infty }$

avec ${\displaystyle a}$ = longueur de l'arête du polyèdre d'origine.

Dodécaèdre fractal

Dodécaèdre fractal après la troisième itération

Le dodécaèdre fractal est le polyèdre fractal platonique dont le volume diminue le plus vite d'une itération à l'autre.

À la limite, sa surface infinie enveloppe un volume nul.

	Volume	Surface
A l'itération n	${\displaystyle {\frac {20^{n}(2+7\varphi /2)}{(2+\varphi )^{3n}}}a^{3}}$	${\displaystyle {\frac {3*20^{n}{\sqrt {5(3+4\varphi )}}}{(2+\varphi )^{2n}}}a^{2}}$
% variation entre deux itérations	${\displaystyle -57,7\%}$	${\displaystyle +53,8\%}$
A l'infini	${\displaystyle Nul}$	${\displaystyle \infty }$

avec ${\displaystyle a}$ = longueur de l'arête du polyèdre d'origine et ${\displaystyle \scriptstyle {\varphi =(1+{\sqrt {5}})/2}}$, le nombre d'or.

Icosaèdre fractal

Icosaèdre fractal après la troisième itération

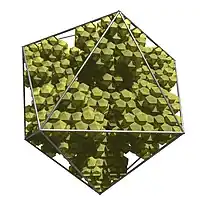
L'icosaèdre fractal est le polyèdre fractal platonique dont la surface augmente le plus vite d'une itération à l'autre.

À la limite, sa surface infinie enveloppe un volume nul.

	Volume	Surface
A l'itération n	${\displaystyle {\frac {5*12^{n}}{6(1+\varphi )^{3n-1}}}a^{3}}$	${\displaystyle {\frac {5*12^{n}{\sqrt {3}}}{(1+\varphi )^{2n}}}a^{2}}$
% variation entre deux itérations	${\displaystyle -33,1\%}$	${\displaystyle +75,1\%}$
A l'infini	${\displaystyle Nul}$	${\displaystyle \infty }$

avec ${\displaystyle a}$ = longueur de l'arête du polyèdre d'origine et ${\displaystyle \scriptstyle {\varphi =(1+{\sqrt {5}})/2}}$, le nombre d'or.

Cube de Cantor

On peut généraliser la construction et ignorer la propriété de connexité en s'autorisant un rapport strictement inférieur à la valeur critique.

Dans ce cas, l'ensemble résultat n'est plus connexe et on ne peut plus parler de polyèdre.

Par exemple, le cube auquel on applique un rapport d'homothétie ${\displaystyle R=1/3}$ conduit à un ensemble disjoint qui, lui, est fractal et a pour dimension ${\displaystyle ln(8)/ln(3)=1,8928}$. Il est baptisé Cube de Cantor.

• Fractale
• Liste de fractales par dimension de Hausdorff

• Les tétraèdres fractals platoniques sur le site de Paul Bourke