Polaire des vitesses

En référence aux travaux en aérodynamique de Otto Lilienthal, on appelle polaire de Lilienthal le tracé du coefficient de portance en fonction du coefficient de traînée, dans le système d'axes liés à la géométrie d'un profil[1] ou à la direction du vol[2].

La polaire des vitesses est une courbe qui présente, pour un appareil ou un profil d'aile donné, la vitesse de vol en abscisse (ou un paramètre lié, tel que le coefficient aérodynamique de traînée C_x) et le taux de chute en ordonnée (ou C_z). Elle permet d'avoir un bon aperçu des performances du profil ou de l'appareil. Cette courbe permet de trouver la finesse maximale théorique, en traçant la tangente à la courbe passant par l'origine.

Polaire des vitesses d'un parapente de type école
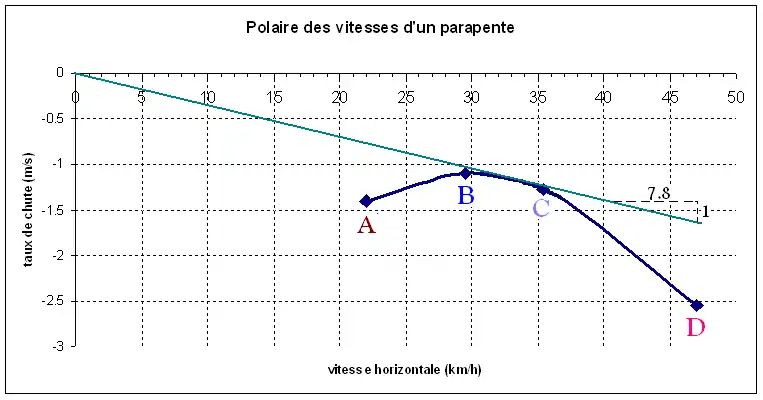
A : vitesse de décrochage
B : Taux de chute mini
C : Finesse max (7,8)
D : vitesse max accélérée

D'après la théorie des profils minces, la polaire des vitesses d'un planeur peut se mettre sous la forme générique[3] :

${\displaystyle w=Av^{3}+{B \over v}}$

où w est la vitesse de chute par rapport à la masse d'air et v est la vitesse horizontale par rapport à la masse d'air.

Un autre type de polaire est la polaire dite d'Eiffel en France. Elle relie le coefficient de portance avec le coefficient de traînée. La traînée totale est la somme de la traînée induite et de la traînée parasite. On peut supposer que le coefficient de traînée parasite ${\displaystyle C_{D_{p}}}$ est une constante. Soit C_L le coefficient de portance.

Le coefficient de traînée induite s'exprime comme suit :

${\displaystyle C_{D_{i}}={C_{L}^{2} \over \lambda e\pi }}$

π (pi) : 3.1416

λ : allongement. Par définition, λ=b²/S où b est l'envergure de l'aile.

e : coefficient d'Oswald (inférieur à 1) qui dépend de la distribution de portance en envergure[Note 1].

e pourrait être égal à 1 pour une distribution de portance « idéale » (elliptique). En pratique e est de l'ordre de 0.75 à 0.85.

La traînée totale est donc :

${\displaystyle C_{D}=C_{D_{i}}+C_{D_{p}}={C_{L}^{2} \over \lambda e\pi }+C_{D_{p}}}$

Donc la courbe qui donne le coefficient de traînée en fonction du coefficient de portance est une parabole qui est quasiment plate. La polaire d'Eiffel représente cette courbe où traditionnellement, l'abscisse est donnée par C_D et l'ordonnée par C_L[5].

Exemple de polaires de vitesse d'un voilier quillard de croisière de 30 pieds pour trois vitesses de vent : 6, 14 et 25 nœuds. Le voilier atteint sa vitesse maximale lorsque la direction du vent réel est comprise entre 120 et 150°. Lorsque la direction du vent se rapproche de la direction du déplacement (entre 0 et 30°) la vitesse du voilier devient nulle.

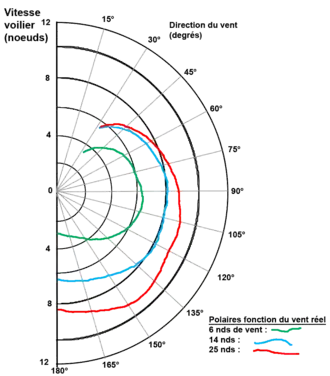
Les voiles et la carène d'un voilier sont également définies par des profils. Le couplage de ces profils l'un aérodynamique et l'autre hydrodynamique détermine quasiment la totalité du comportement d'un voilier. L'influence du fardage est généralement négligeable par rapport à ces deux profils. Un voilier est donc également caractérisé par une polaire des vitesses.

La vitesse du navire est représentée suivant l'angle du vent réel par rapport à la direction de déplacement du voilier : de 0 degré (le vent arrive face au bateau) à 180 degrés (le vent arrive par l'arrière).

• La polaire est tracée pour plusieurs vitesses du vent.
• Pour une même vitesse de vent, plusieurs polaires peuvent être fournies en fonction du jeu de voiles caractérisées principalement par la surface et la forme (par exemple polaire avec un génois ou avec un spi.
• Les polaires dépendent de la forme de la carène, du plan de voilure et du jeux de voiles. Elles sont donc spécifiques à un type de voilier donné.
• Les polaires fournies par les constructeurs correspondent à des conditions de navigation idéales rarement atteintes : carène parfaitement propre, jeu de voiles neuf, mer plate (ou permettant le surf au portant), voile parfaitement adaptée à la vitesse et la direction du vent, absence d'erreur de barre.
• La représentation des données est soit sous forme graphique (ci-contre) soit sous forme de tableau.
• Lorsque le voilier déjauge, c'est-à-dire que la carène se soulève grâce à la vitesse atteinte (voilier de course caractérisé par un rapport surface de voile/poids important) ou en dévalant une vague (surf), la vitesse du navire peu dépasser les valeurs fournies par la polaire car le comportement de la carène est modifié.

Comme le bateau se déplace, il crée un vent relatif (ou vent vitesse, ou encore vent dû à la vitesse) qui se cumule vectoriellement avec le vent réel (ou vent météo) que l'on ressent lorsqu'on est géographiquement immobile[6]. Ce cumul est appelé Vent apparent et est le vent vraiment ressenti par les occupants du bateau en mouvement.

Il faut donc faire attention aux valeurs reportées, vent réel ou apparent, angle du vent réel ou apparent. Les notations couramment employées sont issues de l'anglais et sont :

• TWS : True Wind Speed : vitesse du vent réel ;
• TWA : True Wind Angle : angle du vent réel ;
• AWS : Apparent Wind Speed : vitesse du vent apparent ;
• AWA : Apparent Wind Angle : angle du vent apparent.

La détermination de ces polaires est faite par l'architecte naval grâce à de puissants ordinateurs. Les simulations issues des logiciels sont de plus en plus proches de la réalité, en conséquence les essais en mer sont de plus en plus rares. L'essai en mer est la méthode à la portée du plaisancier. Les essais demandent de la discipline des moyens de mesure fiables tels que le GPS différentiel. Un point de la polaire n'est pas déterminé avec un seul essai mais grâce à un bon nombre d'essais pour en faire la moyenne.

La polaire du voilier est enregistrée dans un logiciel spécialisé qui couplé avec les informations météo, permet par calcul de définir la route la plus rapide vers la destination.

Deux types de logiciels existent :

• les routeurs utilisés par les navigateurs en compétition pour établir leur route ;
• les jeux de simulation de voile tel que Virtual Regatta et surtout Océan Virtuel qui propose l'affichage des polaires de vitesses pour tous les voiliers de course ainsi qu'une table de calcul de la VMG.

• [Paths of Soaring Flight] (en) Frank Irving, The Paths of Soaring Flight, Imperial College Press, 1999, 131 p. (ISBN 978-1-86094-055-2)
• [Naval Aviators] (en) Hugh Harrison Hurt, Aerodynamics for naval aviators, US Navy, 1959, 416 p. (ISBN 978-1-939878-18-2, lire en ligne)