Point de bulle

En thermodynamique, le point de bulle d'un liquide composé d'au moins deux composants correspond aux conditions de pression et de température dans lesquelles les premières bulles de gaz apparaissent[1] - [2] - [3].

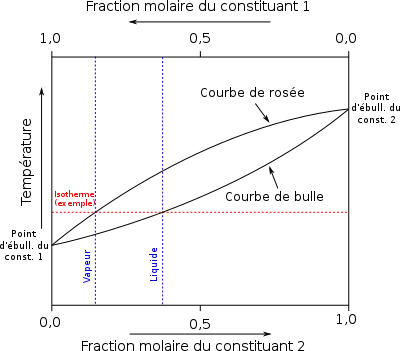
Diagramme binaire liquide-vapeur : courbe de bulle et courbe de rosée.

Pour les substances pures, le point de bulle et le point de rosée coïncident et sont appelés point d'ébullition. À cette température, la pression correspond à la pression de vapeur saturante.

Étant donné que la vapeur aura probablement une composition différente de celle du liquide, le point de bulle (ainsi que le point de rosée) à différentes compositions sont des données utiles lors de la conception de systèmes de distillation[4].

Calcul

Au point de bulle, la relation suivante est valable :

\sum _{i=1}^{N_{c}}y_{i}=\sum _{i=1}^{N_{c}}K_{i}x_{i}=1

où

K_{i}\equiv {\frac {y_{ie}}{x_{ie}}}

K est le coefficient de distribution ou facteur K, défini comme le rapport de la fraction molaire dans la phase vapeur ${\big (}y_{ie}{\big )}$ à la fraction molaire dans la phase liquide ${\big (}x_{ie}{\big )}$ à l'équilibre.

Lorsque la loi de Raoult et la loi de Dalton s'appliquent au mélange, le facteur K est défini comme le rapport de la pression de vapeur sur la pression totale du système [2] :

K_{i}={\frac {P'_{i}}{P}}

Compte tenu de $x_{i}$ ou $y_{i}$ et de la température ou de la pression d'un système à deux composants, des calculs peuvent être effectués pour déterminer les informations inconnues[5].

Références

ISO 7504:2015(fr) Analyse des gaz — Vocabulaire
McCabe, Warren L.; Smith, Julian C.; Harriot, Peter (2005), Unit Operations of Chemical Engineering (seventh ed.), New York: McGraw-Hill, pp. 737–738, (ISBN 0-07-284823-5)
Smith, J. M.; Van Ness, H. C.; Abbott, M. M. (2005), Introduction to Chemical Engineering Thermodynamics (seventh ed.), New York: McGraw-Hill, p. 342, (ISBN 0-07-310445-0)
Perry, R.H.; Green, D.W., eds. (1997). Perry's Chemical Engineers' Handbook (7th ed.). McGraw-hill. (ISBN 0-07-049841-5).
Smith, J. M.; Van Ness, H. C.; Abbott, M. M. (2005), Introduction to Chemical Engineering Thermodynamics (seventh ed.), New York: McGraw-Hill, p. 351, (ISBN 0-07-310445-0)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.