Paradoxe de Stein

Le paradoxe de Stein est un résultat de statistique, dû au statisticien Charles Stein, exposé dans un article de 1956[1], puis étendu dans un article co-écrit avec Willard James en 1961[2]. Ce résultat n'est pas paradoxal à proprement parler, mais surprenant et contre intuitif. Il constitue un pas important dans l'introduction des estimateurs contractants (en) (shrinkage estimators en anglais) en montrant que l'estimateur de James-Stein (en) domine strictement l'estimateur du maximum de vraisemblance. Son caractère paradoxal vient du fait qu'il justifie de combiner des observations sans rapport entre elles pour estimer leurs espérances.

Énoncé

Soient $X_{1},\cdots ,X_{n}$ $n$ variables aléatoires réelles indépendantes ayant des distributions normales d'espérances $\mu _{1},\cdots ,\mu _{n}$ , et toutes de variance $1$ . Le paradoxe concerne l'estimation des espérances $\mu _{1},\cdots ,\mu _{n}$ .

Il est facile de montrer que l'estimateur du maximum de vraisemblance estime $\mu _{1}$ par $X_{1}$ , $\mu _{2}$ par $X_{2}$ , ... , $\mu _{n}$ par $X_{n}$ .

Notons $X$ le vecteur aléatoire de $\mathbb {R} ^{n}$ ayant pour coordonnées $X_{1},\cdots ,X_{n}$ et ${\vec {\mu }}$ le vecteur de $\mathbb {R} ^{n}$ ayant pour coordonnées $\mu _{1},\cdots ,\mu _{n}$ . L'estimateur du maximum de vraisemblance de ${\vec {\mu }}$ est alors simplement ${\hat {\mu }}_{MV}=X$ . Cet estimateur est non biaisé, et il s'agit de l'estimateur non biaisé de plus petite variance. Cependant, le paradoxe de Stein est que si $n\geq 3$ , il existe un meilleur estimateur : l'estimateur de James-Stein (nommé d'après Willard James et Charles Stein), défini par ${\hat {\mu }}_{JS}=\left(1-{\frac {n-2}{\lVert X\rVert ^{2}}}\right)X$ , où $\lVert X\rVert ^{2}=X_{1}^{2}+\cdots +X_{n}^{2}$ est le carré de la norme de $X$ .

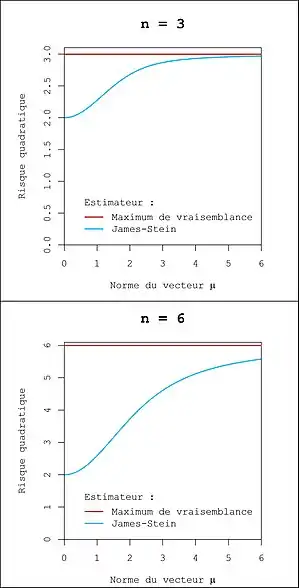
Le mot meilleur ici est à prendre au sens du risque quadratique. Le risque quadratique d'un estimateur ${\hat {\mu }}$ est défini par : $R({\hat {\mu }},{\vec {\mu }})=\mathbb {E} \left(\lVert {\hat {\mu }}-{\vec {\mu }}\rVert ^{2}\right)$ (ce risque correspond à une erreur quadratique moyenne multiparamétrique). L'estimateur de James-Stein est meilleur au sens qu'il a un plus faible risque quadratique que l'estimateur du maximum de vraisemblance, et ce quel que soit ${\vec {\mu }}$ . On dit que l'estimateur de James-Stein domine l'estimateur du maximum de vraisemblance. Cette domination est stricte car il existe des valeurs de ${\vec {\mu }}$ pour lesquelles le risque de l'estimateur de James-Stein est strictement plus petit que celui de l'estimateur du maximum de vraisemblance.

Énoncé formel

Ce résultat peut être énoncé de manière plus concise:

Théorème — Soit $n\geq 3$ , ${\vec {\mu }}\in \mathbb {R} ^{n}$ et $X\sim {\mathcal {N}}({\vec {\mu }},I_{n})$ . Soit ${\hat {\mu }}_{MV}=X$ et ${\hat {\mu }}_{JS}=\left(1-{\frac {n-2}{\lVert X\rVert ^{2}}}\right)X$ . Alors $\mathbb {E} \left(\lVert {\hat {\mu }}_{JS}-{\vec {\mu }}\rVert ^{2}\right)\leq \mathbb {E} \left(\lVert {\hat {\mu }}_{MV}-{\vec {\mu }}\rVert ^{2}\right)$ . De plus, il existe au moins un ${\vec {\mu }}$ pour lequel l'inégalité précédente est stricte.

Démonstration

Reprenons les notations précédentes et calculons le risques quadratiques des deux estimateurs.

Risque quadratique de l'estimateur du maximum de vraisemblance

Le risque quadratique de ${\hat {\mu }}_{MV}$ vaut $n$ :

\mathbb {E} (\lVert {\hat {\mu }}_{MV}-\mu \rVert ^{2})=\mathbb {E} (\lVert X-\mu \rVert ^{2})=\mathbb {E} \left(\sum _{i}^{n}(X_{i}-\mu _{i})^{2}\right)=\sum _{i}^{n}\mathbb {E} \left((X_{i}-\mu _{i})^{2}\right)=\sum _{i}^{n}\mathrm {Var} (X_{i})=n

Risque quadratique de l'estimateur de James-Stein

Le risque quadratique de ${\hat {\mu }}_{JS}$ est

\mathbb {E} (\lVert {\hat {\mu }}_{JS}-\mu \rVert ^{2})=\mathbb {E} \left(\lVert \left(1-{\frac {n-2}{\lVert X\rVert ^{2}}}\right)X-\mu \rVert ^{2}\right)

qu'on peut réécrire

\mathbb {E} \left(\lVert (X-\mu )-{\frac {n-2}{\lVert X\rVert ^{2}}}X\rVert ^{2}\right)

Or,

\lVert (X-{\vec {\mu }})-{\frac {n-2}{\lVert X\rVert ^{2}}}X\rVert ^{2}=\lVert X-{\vec {\mu }}\rVert ^{2}+{\frac {(n-2)^{2}}{\lVert X\rVert ^{2}}}-2(n-2)(X-{\vec {\mu }})\cdot {\frac {X}{\lVert X\rVert ^{2}}}

où

\cdot

désigne le produit scalaire.

Donc

\mathbb {E} (\lVert {\hat {\vec {\mu }}}_{JS}-{\vec {\mu }}\rVert ^{2})=n+(n-2)^{2}\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)-2(n-2)\mathbb {E} \left((X-{\vec {\mu }})\cdot {\frac {X}{\lVert X\rVert ^{2}}}\right)

Calculons maintenant $\mathbb {E} \left((X-{\vec {\mu }})\cdot {\frac {X}{\lVert X\rVert ^{2}}}\right)$ .

{\begin{aligned}\mathbb {E} \left((X-{\vec {\mu }})\cdot {\frac {X}{\lVert X\rVert ^{2}}}\right)&=\sum _{i=1}^{n}\mathbb {E} \left({\frac {X_{i}}{\lVert X\rVert ^{2}}}(X_{i}-\mu _{i})\right)\\&=\sum _{i=1}^{n}\int _{{\vec {x}}\in \mathbb {R} ^{n}}{\frac {x_{i}}{\lVert {\vec {x}}\rVert ^{2}}}{\frac {(x_{i}-\mu _{i})}{(2\pi )^{\frac {n}{2}}}}e^{-{\frac {1}{2}}\lVert {\vec {x}}-{\vec {\mu }}\rVert ^{2}}\mathrm {d} x_{1}\cdots \mathrm {d} x_{n}\end{aligned}}

Chaque intégrale de cette somme peut-être simplifiée en utilisant une intégration par partie en écrivant :

{\frac {(x_{i}-\mu _{i})}{(2\pi )^{\frac {n}{2}}}}e^{-{\frac {1}{2}}\lVert {\vec {x}}-{\vec {\mu }}\rVert ^{2}}={\frac {\partial }{\partial x_{i}}}\left[-{\frac {1}{(2\pi )^{\frac {n}{2}}}}e^{-{\frac {1}{2}}\lVert {\vec {x}}-{\vec {\mu }}\rVert ^{2}}\right]

{\frac {\partial }{\partial x_{i}}}\left[{\frac {x_{i}}{\lVert {\vec {x}}\rVert ^{2}}}\right]={\frac {\lVert {\vec {x}}\rVert ^{2}-2x_{i}^{2}}{\lVert {\vec {x}}\rVert ^{4}}}

D'où

{\begin{aligned}\mathbb {E} \left({\frac {X_{i}}{\lVert X\rVert ^{2}}}(X_{i}-\mu _{i})\right)&=\int _{{\vec {x}}\in \mathbb {R} ^{n}}{\frac {\lVert x\rVert -2x_{i}^{2}}{\lVert {\vec {x}}\rVert ^{4}}}{\frac {1}{(2\pi )^{\frac {n}{2}}}}e^{-{\frac {1}{2}}\lVert {\vec {x}}-{\vec {\mu }}\rVert ^{2}}\mathrm {d} x_{1}\cdots \mathrm {d} x_{n}\\&=\mathbb {E} \left({\frac {\lVert X\rVert ^{2}-2X_{i}^{2}}{\lVert X\rVert ^{4}}}\right)\\&=\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)-2\mathbb {E} \left({\frac {X_{i}^{2}}{\lVert X\rVert ^{4}}}\right)\end{aligned}}

En sommant sur $i$ , on obtient que

\mathbb {E} \left((X-{\vec {\mu }})\cdot {\frac {X}{\lVert X\rVert ^{2}}}\right)=(n-2)\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)

Et donc, le risque de l'estimateur de James-Stein est

n+(n-2)^{2}\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)-2(n-2)^{2}\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)=n-(n-2)^{2}\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)

Étant donné que $\mathbb {E} \left({\frac {1}{\lVert X\rVert ^{2}}}\right)>0$ , on a ainsi que le risque quadratique de l'estimateur de James-Stein est strictement inférieur à celui du maximum de vraisemblance.

Remarques

On remarque que le risque de l'estimateur de James-Stein ne dépend que la norme de ${\vec {\mu }}$ , et qu'il atteint sa valeur minimale, 2, lorsque ${\vec {\mu }}=0$ . En effet, ${\frac {1}{\lVert X\rVert ^{2}}}$ suit alors une Loi inverse χ² d'espérance $n-2$ , donnant alors le risque $R({\hat {\mu }}_{JS},{\vec {\mu }}=0)=2$ . Pour toute valeur de ${\vec {\mu }}$ , le gain d'utiliser l'estimateur de James-Stein augmente avec $n$ .

Interprétation

Paradoxe

Ce résultat est qualifié de paradoxe car il serait naturel de s'attendre à ce que l'estimateur du maximum de vraisemblance soit meilleur. En effet, l'estimation de $\mu _{1}$ dans l'estimateur de James-Stein utilise toutes les observations, même si $X_{2},\cdots ,X_{n}$ ne sont porteurs d'aucune information sur $\mu _{1}$ puisque leurs distributions ne dépendent pas de $\mu _{1}$ et qu'elles sont indépendantes de $X_{1}$ . Il en va de même pour les estimations de $\mu _{2},\cdots ,\mu _{n}$ . Les variables aléatoires $X_{1},\cdots ,X_{n}$ n'ayant possiblement aucun rapport, il est étrange que la meilleure stratégie ne soit pas d'estimer l'espérance $\mu _{i}$ en utilisant uniquement l'observation $X_{i}$ .

Pour illustrer cela[3], supposons qu'on s'intéresse à la proportion d'électeurs qui comptent voter pour Trump à une élection, à la proportion de nouveau-nés filles en Chine, et à la proportion de britanniques ayant les yeux bleus. Pour cela, on dispose de trois observations : le résultat d'un sondage électoral, le nombre de filles nées dans un hôpital chinois et le nombre de personnes aux yeux bleus dans une ville anglaise (ces observations sont issues de lois binomiales, mais elles peuvent facilement être approximées, après transformation, par des lois normales). Alors, en utilisant l'estimateur de James-Stein, on estimera en particulier la proportion de votant pour Trump en utilisant le nombre de filles nées dans l'hôpital chinois et le nombre de personnes aux yeux bleus dans la ville anglaise !

Explication

En réalité, il serait peu judicieux d'utiliser l'estimateur de James-Stein dans l'exemple précédent. Cet estimateur a certes le plus petit risque quadratique combiné sur les trois estimations, mais il n'a pas le plus petit risque quadratique pour une estimation particulière. En général, l'estimateur de James-Stein a tendance à dégrader la plupart des estimations mais à en améliorer sensiblement quelques-unes, ces quelques améliorations compensent les dégradations. Dans l'exemple précédent, il est probable que deux des trois estimations soient moins bonnes avec l'estimateur de James-Stein qu'avec le maximum de vraisemblance, mais que la troisième soit suffisamment meilleure pour réduire le risque quadratique total. En pratique, un statisticien intéressé uniquement à la proportion de filles parmi les nouveau-nés en Chine n'aurait très certainement pas intérêt à utiliser cet estimateur comme décrit précédemment, de même pour quelqu'un intéressé uniquement par la proportion d'électeurs de Trump ou uniquement par le nombre de personnes aux yeux bleus. Pour que cet estimateur ait un intérêt, il faut qu'un statisticien soit intéressé simultanément à ces trois estimations, ce qui est peu probable.

Estimateur contractant

L'estimateur de James-Stein est un exemple d'estimateur contractant (en), c'est-à-dire qui ramène artificiellement les valeurs estimées vers 0. D'autres exemple de tels estimateurs sont les estimateurs de type Lasso ou ceux utilisant une régularisation de Tikhonov (Ridge regression en anglais). Il est donc naturel que le gain de risque quadratique obtenu en utilisant l'estimateur de James-Stein plutôt que le maximum de vraisemblance soit maximal lorsque ${\vec {\mu }}=0$ .

Le risque quadratique d'un estimateur peut se décomposer en $R({\hat {\mu }},{\vec {\mu }})=\lVert \mathbb {E} ({\hat {\mu }})-{\vec {\mu }}\rVert ^{2}+\mathrm {tr} \left(\mathrm {Var} \left({\hat {\mu }}\right)\right)$ . Le premier terme de cette décomposition augmente avec le biais de l'estimateur et le second avec sa variance. La contraction des estimations a pour effet d'augmenter le biais mais de diminuer la variance. La diminution de variance surpasse l'augmentation du biais de telle sorte que le risque quadratique diminue.

Le choix de contracter vers 0 est arbitraire et des estimateurs de James-Stein peuvent être construits en contractant vers n'importe quelle valeur ${\vec {\mu }}_{0}$ selon:

${{\hat {\mu }}_{JS}}^{{\vec {\mu }}_{0}}={\vec {\mu }}_{0}+\left(1-{\frac {1}{\lVert X-{\vec {\mu }}_{0}\rVert ^{2}}}\right)(X-{\vec {\mu }}_{0})$ .

Quelle que soit la valeur de ${\vec {\mu }}_{0}$ , l'estimateur de James Stein contractant vers ${\vec {\mu }}_{0}$ domine strictement le maximum de vraisemblance. Bradley Efron et Carl MorrisCarl Morris ont montré en 1973[4], qu'utiliser ${\vec {\mu }}_{0}=\left({\begin{matrix}{\overline {X}}\\\vdots \\{\overline {X}}\end{matrix}}\right)$ lorsque $n\geq 4$ est un meilleur choix que ${\vec {\mu }}_{0}=0$ .

Généralisations du résultat

L'estimateur de James-Stein peut facilement être amélioré en prenant la partie positive du facteur de contraction donnant l'estimateur : ${{\hat {\mu }}_{JS}}^{+}={\left(1-{\frac {1}{\lVert X\rVert ^{2}}}\right)}_{+}X$ où $(\ \cdot \ )_{+}$ désigne la partie positive.

Le résultat de Stein de 1956 utilise 3 hypothèses : les $X_{i}$ ont des distributions normales, leurs variances sont connues et identiques, et ils sont indépendants. Cependant ce résultat a été étendu et toutes ces hypothèses ne sont pas nécessaires : le paradoxe de Stein a été généralisé à des problèmes d'estimations où les variances des différentes variables aléatoires peuvent être différentes et inconnus, et même à des problèmes où les distributions ne sont pas normales.

L'utilisation du risque quadratique n'est pas indispensable non plus. L'estimateur de James-Stein peut être adapté à une large classe de fonctions de risque pour lesquelles il domine toujours l'estimateur du maximum de vraisemblance[5].

Références

(en) Charles Stein, « Inadmissibility of the Usual Estimator for the Mean of a Multivariate Normal Distribution », Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, The Regents of the University of California,‎ 1956 (lire en ligne, consulté le 2 septembre 2020)
(en) Willard James et Charles Stein, « Estimation with quadratic loss », Breakthroughs in statistics,‎ 1992, p. 443-460 (lire en ligne)
(en) Richard J. Samworth, « Stein's Paradox », Eureka,‎ octobre 2012, p. 38-41 (lire en ligne)
(en) Bradley Efron et Carl Morris, « Stein's Estimation rule and its competitors - an empirical Bayes approach », Journal of the American Statistical Association,‎ mars 1973 (lire en ligne)
Lawrence D. Brown, « On the Admissibility of Invariant Estimators of One or More Location Parameters », Annals of Mathematical Statistics,‎ 1966 (lire en ligne)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.