Paradoxe d'Ehrenfest

On montre (voir l'effet Sagnac) que la circonférence d'un disque tournant est différente vue dans le repère inertiel R et dans le repère R' attaché au disque tournant, à cause de la contraction de Lorentz.

Mais comme le rayon du disque est perpendiculaire au mouvement de rotation, il ne subit pas de contraction de Lorentz.

Par conséquent, le rapport ${\displaystyle L/R}$ entre le périmètre et le rayon est différent de ${\displaystyle 2\pi }$ dans un des deux repères.

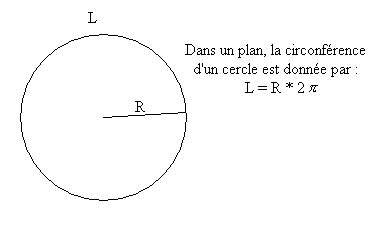
R étant un repère inertiel, l'espace est euclidien, comme le montre la relativité restreinte (contrairement à l'espace-temps qui n'est pas euclidien mais de Minkowski). Et le disque, en rotation ou pas, est un cercle obéissant à la géométrie d'Euclide avec un rapport ${\displaystyle L/R=2\pi }$. Et donc :

${\displaystyle L'/R'\neq 2\pi }$

C'est le paradoxe d'Ehrenfest[2] : dans un repère en rotation, le rapport entre la circonférence et le diamètre est différent de ${\displaystyle \pi }$. Si la géométrie était euclidienne dans R', le disque serait « voilé » ou « déchiré ».

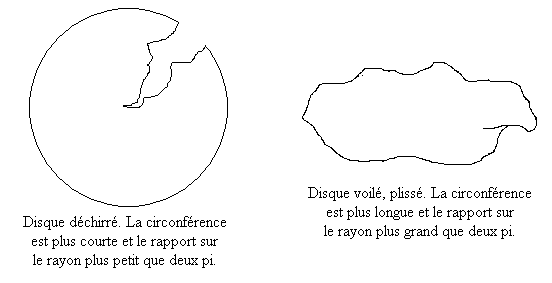
Mais il ne l'est pas, d'une part parce que nous considérons une rotation « en bloc » mais surtout parce que ce disque est « virtuel » : ce qui nous importe c'est le repère en rotation, le système de coordonnées en rotation, et non spécialement un disque physique que l'on mettrait en rotation à grande vitesse. D'ailleurs un observateur O' placé au bord du disque peut très bien tourner en cercle sans avoir besoin de ce disque. La géométrie n'est donc pas euclidienne dans R'.

Avec les raisonnements simples vus dans l'effet Sagnac, on constate que la circonférence est plus grande dans R'. La géométrie y est donc hyperbolique.

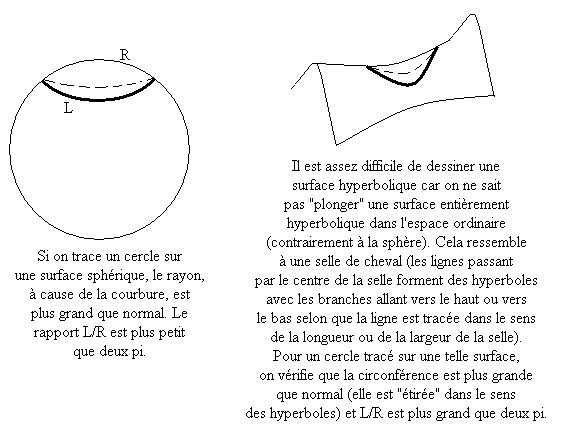
La géométrie étant non euclidienne, il est difficile de garantir que diviser la longueur du cercle (considéré d'un point de vue euclidien) par le temps de parcours autour du cercle conduit bien à une vitesse identique à une vitesse mesurée localement. Cela justifie le terme de vitesse apparente qui a été utilisé dans l'article sur l'effet Sagnac.

D'autre part, le mot paradoxe est bien choisi car un des postulats utilisé dans ces raisonnements simples, mais aussi en relativité restreinte, est que l'espace est euclidien. Toutefois, la relativité restreinte est construite pour des repères inertiels (ou accélérés dans des domaines infinitésimaux où il est toujours possible de trouver un espace plat tangent, tout comme il existe toujours une droite tangente en un point du cercle). Il se peut que pour des repères accélérés ce postulat ne soit pas tenable.

Nous avons écrit que le paradoxe tenait au fait que l'espace physique considéré (l'espace occupé par le disque) était le même dans les deux repères. Mais en relativité restreinte, nous ne pouvons pas séparer arbitrairement l'espace du temps. Ainsi, ce qui est identique pour les deux repères est l'espace-temps physique constitué du continuum d'événements (par exemple le passage de O' en un point donné à un instant donné) et décrit par la géométrie de Minkowski. Nous n'avons aucune garantie que, en considérant uniquement la partie spatiale de l'espace-temps, l'espace reste euclidien dans R'.

L'analyse approfondie de ce qui se passe peut être trouvée dans le calcul de l'effet Sagnac en relativité restreinte et dans la géométrie de l'espace-temps dans les repères tournants.

Le disque en rotation a joué un rôle important dans le développement de la relativité générale par Albert Einstein, et l'a notamment amené à utiliser une géométrie non euclidienne pour décrire les effets de la gravitation.

Disque d'Einstein - Pour un observateur au repos, les règles disposées sur la périphérie subissent une contraction : un plus grand nombre de règles est donc nécessaire sur le disque pour couvrir l'ensemble du périmètre.

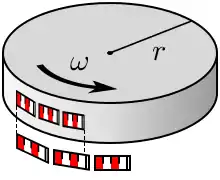
L'expérience de pensée proposée par Einstein diffère cependant de celle d'Ehrenfest[1] - [5] : alors qu'Ehrenfest considère une situation impossible où un disque immobile est mis en rotation de manière rigide, Einstein considère un disque initialement en rotation uniforme, sans imposer de contrainte particulière sur l'obtention de cet état initial (une lettre de 1910 indique qu'Einstein était au courant des résultats d'Herglotz sur les restrictions imposées à la rotation des corps rigides en relativité).

En raison de la dilatation des durées, il note tout d'abord qu'une horloge fixée sur la périphérie semblera retarder pour un observateur au repos situé au centre du disque. Il conclut par ailleurs qu'un physicien situé sur la circonférence et solidaire du mouvement mesurera un périmètre supérieur à ${\displaystyle \pi }$ fois le diamètre (${\displaystyle P>\pi D}$), car sa règle subira une contraction des longueurs dans la direction parallèle au mouvement mais pas dans la direction perpendiculaire[note 1] (Einstein fait ici l'hypothèse importante que la règle est rigide et que son comportement dépend uniquement de la vitesse et non de l'accélération, en d'autres termes elle se comporte momentanément comme une règle en translation rectiligne uniforme). Ce résultat étant contradictoire avec les lois habituelles de la géométrie, il en déduit que la géométrie cesse d'être euclidienne dans le repère en rotation.

Par ailleurs, en vertu du principe d'équivalence, un habitant du disque peut très bien considérer que celui-ci est immobile et que la force centrifuge qu'il ressent résulte de l'action d'un champ de gravité externe. Par conséquent, Einstein conclut que tout champ de gravité déforme la géométrie de l'espace-temps, et que la généralisation de la relativité à tous les référentiels nécessite d'utiliser les outils de la géométrie riemannienne.