Nombre métallique
En mathématiques, les nombres métalliques (ou constantes métalliques) forment une suite de nombres réels généralisant le nombre d'or. Il a été proposé deux généralisations possibles.
Introduction pour la première généralisation
Le nombre d'or permettant d'exprimer le terme général des suites vérifiant la récurrence linéaire définissant la suite de Fibonacci , il a été proposé d'appeler nombres métalliques les nombres permettant d'exprimer, pour un nombre entier p, le terme général des suites vérifiant la récurrence linéaire :
Par définition, le p-ième nombre métallique, noté , est l'unique solution positive de l'équation caractéristique de la récurrence : .
Si une telle suite tend vers l'infini, est la limite du rapport .
Pour p = 2, le métal proposé a été l'argent, puis le bronze pour le nombre suivant[1] - [2] - [3].
Diverses expressions
- En tant que solution positive de l'équation du second degré , on obtient l'expression analytique du nombre métallique d'indice p :
- .
- En réécrivant l'équation sous la forme
on en déduit son développement en fraction continue :
- .
- En réécrivant l'équation sous la forme
on en déduit sa forme en radical imbriqué infini :
- .
- Le p-ième nombre métallique est également donné par une intégrale :
Rectangles métalliques
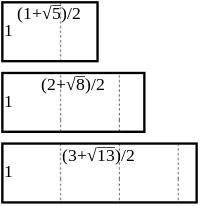
Le p-ième nombre métallique est le rapport entre la longueur et la largeur d'un rectangle tel que si on lui ôte p carrés de taille maximale, on obtient un rectangle semblable à celui de départ.
On obtient en effet la relation qui donne si on pose .
Premières valeurs
| p | Expression | Écriture décimale | Métal associé | Suite récurrente associée |
|---|---|---|---|---|
| 1 | 1,618033989 | Or | suite de Fibonacci | |
| 2 | 1 + √2 | 2,414213562 [note 1] | Argent | suite de Pell |
| 3 | 3 + √132 | 3,302775638 [note 2] | Bronze | suite A006190 de l'OEIS |
| 4 | 2 + √5 | 4,236067978 [note 3] | suite A001076 de l'OEIS | |
| 5 | 5 + √292 | 5,192582404 [note 4] | suite A052918 de l'OEIS | |
| 6 | 3 + √10 | 6,162277660 [note 5] | suite A005668 de l'OEIS | |
| 7 | 7 + √532 | 7,140054945 [note 6] | ||
| 8 | 4 + √17 | 8,123105626 [note 7] | ||
| 9 | 9 + √852 | 9,109772229 [note 8] | ||
| ⋮ | ||||
| p | p + √4 + p22 | |||
Expressions trigonométriques
| Numéro du nombre métallique | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Formule trigonométrique | ||||
| Polygone régulier associé | Pentagone | Octogone | Tridécagone | 29-gone |
Propriétés des puissances entières
Puissances entières
De même que les puissances successives du nombre d'or vérifient où est la suite de Fibonacci, les puissances des nombres métalliques vérifient :
où la suite , définie par est la p-suite de Fibonacci.
En prolongeant la suite aux entiers négatifs et en acceptant les négatifs dans la définition de , la relation (1) est valable pour tous les entiers relatifs.
Alors, si est l'autre solution de , les puissances de vérifient également de sorte que, par application de la formule de Binet, on a l'égalité :
- .
Remarquons aussi que puisque , l'inverse d'un nombre métallique a la même partie fractionnaire que lui.
De plus, la propriété se généralise. En effet, toute puissance impaire d'un nombre métallique est un autre nombre métallique :
Par exemple, .
Deuxième généralisation : constantes de p-nacci.
Une autre généralisation de la récurrence linéaire double : étant la récurrence p-uple : , il a été aussi proposé d'appeler nombres métalliques les nombres permettant d'exprimer le terme général des suites vérifiant cette récurrence. Partant de l'or, l'argent et le cuivre (situés au-dessus de l'or dans le tableau périodique), ont été proposés pour les nombres suivants : le nickel, le cobalt et le fer [4] - [5] - [6]. Mais par conformité avec les appellations données dans l'encyclopédie des suites entières (OEIS), nous désignerons ces nombres par constantes de p-nacci.
Par définition, chaque constante, notée dans [4], est l'unique solution positive de l'équation caractéristique de la récurrence : (attention, avec cette numérotation, le nombre d'or est , étant égal à 1).
En utilisant la formule des suites géométriques, on obtient que est l'unique solution positive autre que 1 de l'équation de degré p + 1 : , équation qui peut s'écrire aussi : . Elle ne s'exprime pas à l'aide de radicaux à partir de p = 5, mais peut s'écrire comme somme d'une série[7] :
Premières valeurs
| p | Constante de | Expression | Écriture décimale | Métal
(appellation de [5]) |
Suite récurrente associée |
|---|---|---|---|---|---|
| 2 | Fibonacci | 1,618033989 | Or | suite de Fibonacci | |
| 3 | Tribonacci | 1,8392867552 | Argent | suite de Tribonacci | |
| 4 | Tétranacci | Existence d'une expression par radicaux réels faisant intervenir
|
1,927561975 | Cuivre | suite de Tétranacci, suite A000078 de l'OEIS |
| 5 | Pentanacci | Pas d'expression par radicaux | 1,9659482366 | Nickel | suite de Pentanacci, suite A001591 de l'OEIS |
| 6 | Hexanacci | " | 1,983582843 | Cobalt | suite d'Hexanacci, suite A001592 de l'OEIS |
| 7 | Heptanacci | " | 1,991964197 | Fer | suite d'Heptanacci, suite A122189 de l'OEIS |
Étude de la suite des constantes de p-nacci
Cette suite croit strictement de 1 jusqu'à sa limite égale à 2. Ceci est aussi "confirmé" par la suite d' "infinacci" où chaque terme est la somme de tous les précédents, débutant par 0,1 : 0, 1, 1, 2, 4, 8, 16, 32, ... où le quotient de termes consécutifs vaut exactement 2.
Un encadrement simple est [4]:
- .
Un développement asymptotique est [4]:
- .
L'équation caractéristique possède une unique solution négative, supérieure à –1 pour 'p' pair, et aucune pour 'p' impair. Cette solution, ainsi que les solutions complexes ont un module vérifiant , qui tend donc vers 1 quand 'p' tend vers l'infini.
Voir également
Notes et références
-
 A014176, Decimal expansion of the silver mean, 1+sqrt(2).
A014176, Decimal expansion of the silver mean, 1+sqrt(2). -
 A098316, Decimal expansion of [3, 3, ...] = (3 + sqrt(13))/2.
A098316, Decimal expansion of [3, 3, ...] = (3 + sqrt(13))/2. -
 A098317, Decimal expansion of phi^3 = 2 + sqrt(5).
A098317, Decimal expansion of phi^3 = 2 + sqrt(5). -
 A098318, Decimal expansion of [5, 5, ...] = (5 + sqrt(29))/2.
A098318, Decimal expansion of [5, 5, ...] = (5 + sqrt(29))/2. -
 A176398, Decimal expansion of 3+sqrt(10).
A176398, Decimal expansion of 3+sqrt(10). -
 A176439, Decimal expansion of (7+sqrt(53))/2.
A176439, Decimal expansion of (7+sqrt(53))/2. -
 A176458, Decimal expansion of 4+sqrt(17).
A176458, Decimal expansion of 4+sqrt(17). -
 A176522, Decimal expansion of (9+sqrt(85))/2.
A176522, Decimal expansion of (9+sqrt(85))/2.
- (en) Vera W. de Spinadel, « The Family of Metallic Means », Vismath, Mathematical Institute of Serbian Academy of Sciences and Arts, vol. 1, no 3, (lire en ligne).
- de Spinadel, « The Metallic Means and Design », Nexus II: Architecture and Mathematics, Fucecchio (Florence), Edizioni dell'Erba, , p. 141–157 (lire en ligne)
- (en) « An Introduction to Continued Fractions: The Silver Means », sur maths.surrey.ac.uk.
- G. Huvent, « Les nombres de Métal : alchimie mathématique de la transformation », Irem de Lille, (lire en ligne)
- Claire FRANCESCONI, « L’étude des nombres métalliques et de leurs figures associées », Irem de La Réunion, (lire en ligne)
- Collectif, « A la suite du nombre d'or, les métalliques », (consulté le )
- D.A. Wolfram, « Solving Generalized Fibonacci Recurrences », Fib. Quart., (lire en ligne)
Bibliographie
- (en) Alexey Stakhov, « The Mathematics of Harmony: Clarifying the Origins and Development of Mathematics », sur PeaceFromHarmony.org.
- (en) Cristina-Elena Hrețcanu et Mircea Crasmareanu, « METALLIC STRUCTURES ON RIEMANNIAN MANIFOLDS », REVISTA DE LA UNION MATEMATICA ARGENTINA, vol. 54, no 2, , p. 15–27 (lire en ligne).
- (en) Miloje M. Rakočević, « FURTHER GENERALIZATION OF GOLDEN MEAN IN RELATION TO EULER’S “DIVINE” EQUATION », sur arxiv.org.









![{\displaystyle \varphi _{p}=p+{\cfrac {1}{p+{\cfrac {1}{p+{\cfrac {1}{p+{\cfrac {1}{p+\ddots \,}}}}}}}}=[p;p,\dots ]}](https://img.franco.wiki/i/e4bd45fc8e5c0dcf35ee341256cbba4264e8ca01.svg)
































![{\displaystyle {\frac {{\sqrt[{3}]{19+3{\sqrt {33}}}}+{\sqrt[{3}]{19-3{\sqrt {33}}}}+1}{3}}}](https://img.franco.wiki/i/a138e45eeecacb9865353220877e19c8900e2785.svg)
![{\displaystyle {\sqrt[{3}]{65+3{\sqrt {1689}}}}}](https://img.franco.wiki/i/6e42fd2ac9f698047afb67a23b216a04bda5dd92.svg)



