Nivellement (topographie)

Les difficultés du nivellement sont de deux types :

Le principal problème à résoudre par le nivellement est celui des écoulements d'eaux. C'est donc un problème physique, et non géométrique. La différence entre une forme théorique de la Terre et la forme réelle des surfaces de niveaux est parfois considérable. Les appareils utilisés jusqu'à une époque très récente étaient tous réglés par une mesure physique (utilisation d'une nivelle ou d'un dispositif équivalent). L'utilisation de mesures GPS oblige aujourd'hui à modéliser le géoïde en recherchant une formule d'interpolation locale qui minimise les écarts constatés sur des repères connus à la fois dans un système géométrique (WGS par exemple) et dans le système physique.

Une autre difficulté tient à la propagation de la lumière dans l'atmosphère : l'air ayant un poids, sa densité décroît avec l'altitude, et ce gradient de densité occasionne un gradient d'indice de réfraction : les rayons lumineux, dans une atmosphère calme et à l'équilibre, sont incurvés vers la terre, dans une mesure qui dépend de la température et de l'altitude. Pour calculer les dénivelés, on doit appliquer une correction aux mesures, et cette correction est intégrée à celle due à la rotondité de la terre qui est de la forme[1] :

${\displaystyle c=qD^{2}}$, avec ${\displaystyle q}$ de l'ordre de 60 × 10⁻⁹ m⁻¹

Nivellement direct ou géométrique

Nivellement indirect ou trigonométrique

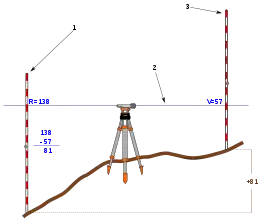
• Le nivellement direct ou géométrique :

Le principe du nivellement géométrique est la mesure d’une différence d’altitude, ou d’une succession de différences, par rapport à un point d'altitude connue, souvent un repère de nivellement. L'altitude du point connu, et les différences d'altitude mesurées, permettent par simple soustraction de déterminer l'altitude des points.

Il est réalisé au niveau de chantier, au niveau optique ou au niveau numérique, et à l'aide d'une mire graduée. Le principe est en fait assez simple, le niveau faisant toujours une lecture à l'horizontale, chaque dénivelé est simplement lu sur la mire qui est tenue à la verticale.

La correction qD² est nulle si le niveau est à égale distance des deux positions de la mire. Ces distances sont mesurées avec une précision suffisante par lecture directe sur la mire, les réticules de tous les niveaux intégrant des repères matérialisant un angle d'un centiradian, les longueurs des portées variant de trente à quatre-vingt mètres selon la précision recherchée.

La précision des mesures peut aller de 1/10 de mm à quelques mm, selon les matériels et protocoles mis en œuvre.

Les niveaux de précisions sont donnés pour un écart-type de 0,3 mm/km de cheminement double.

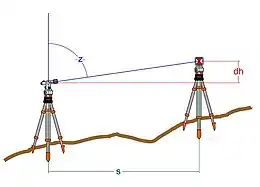
• Le nivellement indirect ou trigonométrique :

Le nivellement trigonométrique est réalisé par calcul du dénivelé et non plus sa mesure directe. On ne mesure plus le dénivelé entre deux points pour déduire une altitude, mais on calcule tout d'abord ce dénivelé grâce à des mesures d'angles et de distances réalisés à l'aide d'un théodolite ou d'un tachéomètre. Selon le matériel et le mode opératoire, on atteint des précisions centimétriques ou décimétriques.

• Le nivellement hydrostatique :

Cette méthode est peu employée, mais permet des mesures de haute précision. Elle est basée sur le principe des vases communicants et permet le calcul de dénivelés par différence de niveau d'un liquide. Elle est principalement utilisée pour le suivi d'ouvrage d'art, comme des barrages par exemple. Elle ne peut s'utiliser qu'en terrain plat, la pression du liquide atteindrait des valeurs élevées si le tuyau venait à se trouver beaucoup plus bas que les ampoules, et de plus elle pourrait donner des résultats erronés si la dilatation de liquide est trop hétérogène, la densité de l'eau variant de 0,6 % entre vingt et quarante degrés Celsius. En revanche elle permet de suivre le cours des fleuves avec une grande précision. C'est le procédé le plus simple, souvent utilisé en maçonnerie.

• Le nivellement barométrique :

Cette méthode relativement imprécise permet le calcul de dénivelés en s'appuyant sur des différences de pressions atmosphériques. Elle est néanmoins très utilisée par le randonneur et par le parapentiste avec un altimètre barométrique.

• Le nivellement par positionnement satellitaire :

Il consiste à déterminer l'altitude d'un point à l'aide des signaux émis par des satellites de positionnement (exemple systèmes GPS, Glonass, Galileo pour le futur). La précision dépend du mode opératoire utilisé lors des mesures, selon que l'on soit en système de positionnement relatif (précision env. ±0,5 à 2 cm) ou absolu (précision ±5 à 100 m).

• Le nivellement photogrammétrique :

Grâce à l'observation sous un stéréorestituteur d'un couple de photographies aériennes figurant la même portion de territoire vue sous deux angles de vue différents, il est possible de déterminer l'altitude d'un point au sol avec une précision variable selon l'altitude de vol, l'objectif utilisé, le type de restituteur, la qualité du film, les aptitudes de l'opérateur en photogrammétrie ; elle peut atteindre ±10 cm dans de bonnes conditions.