Nématicon

En optique, un nématicon est un soliton spatial dans des cristaux liquides nématiques. Le nom a été inventé en 2003 par G. Assanto[1]. et s'est imposé par la suite [2] - [3]. Les nématicons sont engendrés par un type spécial de non-linéarité optique présent dans les nématiques : la réorientation induite par la lumière du vecteur directeur moléculaire, c'est-à-dire de la moyenne de l'orientation moléculaire. Cette non-linéarité provient du fait que le vecteur directeur moléculaire (qui est l'axe optique de l'uniaxe correspondant) tend à s'aligner le long du champ électrique de la lumière. Les nématicons sont faciles à engendrer avec des puissances optiques  de quelques mW ou moins [4] - [5] - [6] car le milieu diélectrique constitué par les cristaux liquides nématiques  possède les propriétés suivantes :

• Une très grande réponse non-linéaire : la non-linéarité est de huit ordres de grandeur plus grande que celle du disulfure de carbone. Cela signifie que des puissances optiques beaucoup plus faibles sont nécessaires pour obtenir la même variation d'indice de réfraction (augmentation) ou d'auto-focalisation permettant de compenser  la diffraction.
• Une réponse non locale : la réponse non linéaire n'est pas limitée à l'emplacement du champ optique. Au lieu de cela, le profil de réponse est plus large que le faisceau lumineux. Une forte non-localité permet la propagation stable de faisceaux solitons, même dans le cas de deux dimensions transversales. Des valeurs supérieure ou inférieure de puissance optique requises pour un soliton conduisent à des solitons respirants[7] - [8] - [9].

Différence entre réponse locale et non-locale. Dans un milieu local un pic de Dirac en intensité donne lieu à une réponse spatiale de l'indice de réfraction tout aussi forte. Dans un milieu non-local la variation de l'indice de réfraction s'étend bien au-delà de la source.

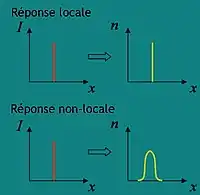
• Une réponse tout-optique saturable : le directeur du cristal liquide a tendance à s'aligner le long du champ électrique de l'onde lumineuse. Pour de puissants faisceaux moléculaires directeur devient parallèle au champ et pas plus loin que la réorientation est possible. Réponse de la saturation stabilise aussi deux dimensions de solitons.

Comme l'orientation de la non-linéarité optique de cristaux liquides nématiques est sensible à l’application de champs électriques de basse fréquence, les nématicons et les guides d'ondes induits [10] peuvent être orientée angulairement et spatialement par l'application d'une tension externe, conduisant à des interconnexions reconfigurables[11] - [12].

Dans les réseaux de guides d'ondes où se forment des solitons discrets[13], des nématicons discrets ont également été observés[14] - [15].