Morphisme zéro

Supposons que C soit une catégorie, et f : X → Y un morphisme de la catégorie C. Le morphisme f est appelé morphisme constant (ou encore morphisme zéro à gauche) si pour tout objet W de la catégorie C et tout morphisme de cette catégorie g, h : W → X, on a fg = fh. Parallèlement, f est appelé morphisme coconstant [1] (ou encore morphisme zéro à droite) si pour tout objet Z de la catégorie C et tout morphisme de cette catégorie g, h : Y → Z, on a gf = hf. Un morphisme zéro est à la fois un morphisme constant et coconstant [1].

Une catégorie avec morphismes zéro est celle où, pour tous les couples d'objets A et B de la catégorie C, il y a un morphisme fixe de cette catégorie 0_AB : A → B, cette collection de morphismes zéro étant telle que pour tous les objets X, Y, Z de la catégorie C et tous les morphismes de cette catégorie f : Y → Z, g : X → Y, le diagramme suivant commute:

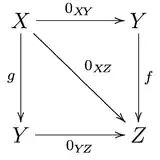
Les morphismes 0_XY sont nécessairement des morphismes zéro et forment un système compatible de morphismes zéro.

Si C est une catégorie avec morphismes zéro, alors la collection des morphismes zéro 0_XY est unique[2].

Cette façon de définir séparément un "morphisme zéro" et l'expression "une catégorie à morphismes zéro" est malheureuse, mais si chaque sous-catégorie a un "morphisme zéro", alors la catégorie est "à morphismes zéro".

• Dans la catégorie des groupes (ou des modules ), un morphisme zéro est un homomorphisme f : G → H qui mappe tout G à l'élément d'identité de H. L'objet zéro dans la catégorie des groupes est le groupe trivial 1 = {1}, qui est unique à un isomorphisme près. Tout morphisme zéro peut être factorisé par 1, c'est-à-dire f : G → 1 → H.
• Plus généralement, supposons que C soit une catégorie avec un objet zéro 0 ${\displaystyle \Rightarrow }$ pour tous les objets X et Y, il existe une séquence unique de morphismes zéro

0_XY : X → 0 → Y

La famille de tous les morphismes ainsi construite confère à C la structure d'une catégorie à morphismes zéro.

• Si C est une catégorie pré-additive, alors tout ensemble de morphismes Mor ( X, Y ) est un groupe abélien et a donc un élément nul. Ces éléments nuls forment une famille compatible de morphismes zéro pour C ce qui en fait une catégorie à morphismes zéro.
• La catégorie des ensembles n'a pas d'objet nul, mais elle a un objet initial, l' ensemble vide ∅. Les seuls morphismes zéro à droite dans cette catégorie sont les fonctions ∅ → X pour un ensemble X.

Si C a un objet zéro 0, étant donné deux objets X et Y de la catégorie C, il existe des morphismes canoniques f : X → 0 et g : 0 → Y. Alors, gf est un morphisme zéro dans Mor _C ( X, Y ). Ainsi, toute catégorie avec un objet zéro est une catégorie avec un morphisme zéro donné par la composition 0_XY : X → 0 → Y.

Si une catégorie a des morphismes zéro, alors on peut définir les notions de noyau et de conoyau [1] pour tout morphisme de cette catégorie.

• Section 1.7 de Bodo Pareigis, Categories and functors, Academic Press, 1970 (ISBN 978-0-08-087352-7 et 0-08-087352-9, OCLC 301317943, lire en ligne)
• Herrlich, Horst; Strecker, George E. (2007), Category Theory, Heldermann Verlag.