Modèle de Jaynes-Cummings
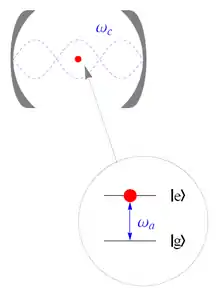
Le modèle de Jaynes–Cummings (en abrégé JCM pour Jaynes-Cummings Model) est un modèle théorique en optique quantique. Il permet de représenter l'interaction lumière/matière dans la mesure où il modélise un système constitué, au sein d'une cavité optique, par un atome à deux niveaux interagissant avec un mode quantifié du champ électromagnétique. Le modèle offre l'avantage de se prêter à des calculs de solutions exactes. En outre, la simplicité de la représentation de l'interaction n'affecte en rien sa capacité à traiter une grande quantité de phénomènes observés.
Historique
À l'origine, ce modèle a été proposé en 1963 par Edwin Jaynes et Fred Cummings dans l'idée de comparer une approche semi-classique du phénomène de l'émission spontanée avec une approche purement quantique de celui-ci[1].
Auparavant, en théorie semi-classique de l'interaction champ-atome, seul l'atome est quantifié alors que le champ est traité comme une fonction définie du temps plutôt que comme un opérateur. La théorie semi-classique permet d'expliquer beaucoup de phénomènes observés en optique moderne, tels par exemple l'existence de cycles de Rabi dans des probabilités d'excitation atomique. Le modèle de Jaynes–Cummings permet de mettre en évidence comment la quantification du champ affecte les prédictions de l'évolution de l'état du système. Il déroule également la dynamique de la résurgence de l'inversion de population atomique après effondrement comme conséquence directe de la discrétisation des états du champ (des photons)[2] - [3]. Ceci est un pur effet quantique qui peut être décrit par le modèle mais pas par la théorie semi-classique.
En 1987, soit 24 ans plus tard, Rempe, Walther et Klein ont observé une belle manifestation de l'effondrement quantique et de ses résurgences dans un maser à un atome prédite par le modèle[4].
Avant cette époque, les équipes de chercheurs n'ont pas pu réunir les conditions expérimentales capables de renforcer le couplage d'un atome avec un seul mode du champ, tout en éteignant simultanément les autres modes. Expérimentalement, le facteur de qualité de la cavité doit être suffisamment élevé pour pouvoir considérer la dynamique du système comme équivalente à celle d'un seul mode du champ. Avec l'apparition de masers à un atome, il devenait possible d'étudier d'un point de vue expérimental l'interaction d'un seul atome (habituellement un atome de Rydberg) avec un seul mode résonant du champ électromagnétique dans une cavité [5] - [6], ainsi que d'étudier différents aspects du modèle de Jaynes–Cummings.
Pour observer un couplage atome-champ fort dans les fréquences de lumière visible, les modes de sabliers optiques peuvent se révéler efficaces à cause de la largeur de leurs spectres de modes favorisant ainsi l'éventualité d'une coïncidence avec un champ fort à l'intérieur de la cavité[7]. Une boîte quantique à l'intérieur d'une nano-cavité photonique de cristal est aussi un système prometteur pour observer l'effondrement et la résurgence de cycles de Rabi dans les fréquences lumineuses du visible[8].
Le modèle a été généralisé de diverses manières afin de décrire précisément l'interaction entre un champ laser et un atome. Ces généralisations consistent tantôt en application de conditions initiales[9], tantôt en la prise en compte dans le modèle d'effets de dissipation et d'amortissements[9] - [10] - [11] , tantôt en la prise en compte d'atomes à niveaux multiples, voire de multiples atomes [12] - [13] et autres descriptions multimodales des champs[14].
On a aussi découvert que pendant les intervalles tranquilles d'oscillations Rabi effondrées l'atome et le champ se trouvent dans un état de superposition (pensez au chat de Schrödinger). Cette découverte offre l'occasion d'utiliser ce modèle pour élucider les propriétés de base de corrélation quantique (l'intrication)[15].
La généralisation du modèle aux atomes avec plus de deux niveaux (l'équivalent de spins supérieurs à 1/2) est connue comme le modèle de Dicke ou le modèle de Tavis-Cummings .
Dans une autre étude, le modèle de Jaynes–Cummings est employé pour modéliser le transfert d'informations quantiques[16].
Deux utilisations majeures
Le travail de thèse effectué par Serge Haroche à l’ENS entre 1967 et 1971 a introduit en physique atomique le concept d’atome habillé par des photons, qui consiste à traiter un atome interagissant avec un champ électromagnétique comme une entité, l’atome habillé, dont l’étude des niveaux d’énergie permet d’analyser de façon simple et synthétique l’ensemble des propriétés physiques. Les états propres du hamiltonien global du modèle de Jaynes–Cummings sont dénommés états habillés dans la littérature[17].
Les oscillations de Rabi ne sont pas seulement liées à l’échange d’énergie entre un atome à deux niveaux et un champ électromagnétique. Le groupe du Professeur Wineland a réalisé une expérience permettant d’observer l’échange d’énergie entre les degrés de libertés externe et interne d’un ion piégé[18]. Lorsque le paramètre de Lamb-Dicke caractérisant le mouvement externe est petit, l’échange d’énergie peut être décrit avec ce modèle[19] - [20].
Formulation du modèle
Le décryptage du montage expérimental illustré en début de cet article, nous amène à formuler un modèle dont l'opérateur hamiltonien décrivant le système dans sa totalité est lui-même formé par la somme de trois opérateurs : un hamiltonien du champ libre, un hamiltonien de l'excitation atomique et un hamiltonien de l'interaction Jaynes–Cummings. On peut l'écrire comme suit :
Description détaillée
Opérateur hamiltonien du champ
Le champ à l'intérieur du résonateur est décrit en termes d'opérateurs de création et d'annihilation bosoniques de photons.
où
- est la constante de Planck réduite ;
- est l'opérateur de création ;
- est l'opérateur d'annihilation ;
- le terme 1/2 représente l'énergie du vide.
Au passage, on reconnaît ici l'opérateur nombre de particules : , de sorte que les valeurs propres d'énergie autorisées du champ, , dépendent de la quantité de photons présents.
Opérateur hamiltonien de l'excitation atomique
L'opérateur hamiltonien pour l'atome seul est donné par
où
- est l'opérateur atomique de montée de l'état fondamental vers l'état excité ;
- est l'opérateur atomique de descente de l'état excité vers l'état fondamental ;
- et représente la fréquence de résonance atomique.
On considère ici l'atome comme un système à deux niveaux. Cela signifie que l'on n'a pas affaire à un atome avec son spin en tant que tel mais bien à un système quantique générique à deux niveaux dont l'espace de Hilbert est isomorphe à un spin demi-entier. Il peut se trouver dans son état fondamental avec l'énergie E=0 ou dans son état excité avec l'énergie .
Si l'on définit l'opérateur d'inversion atomique comme le commutateur des opérateurs atomiques de montée et de descente
alors l'hamiltonien de l'excitation atomique peut s'écrire comme
Opérateur hamiltonien d'interaction
Enfin, on décrit l'interaction entre champ et atome par un hamiltonien d'interaction
où
- est l'opérateur du champ;
- est l'opérateur de polarisation.
Pour comprendre pourquoi et comment on peut simplifier l'expression de l'hamiltonien d'interaction à l'aide de l'approximation des ondes tournantes, il convient de suivre le raisonnement suivant.
On part de l'hamiltonien du modèle (semi-classique) de Rabi formulé comme suit :
C'est un modèle semi-classique dans la mesure où
- est l'opérateur quantique du moment dipolaire de l'atome;
- est le champ électrique classique tel que .
Notons que dans le modèle de Rabi, le champ électromagnétique est libre.
On peut maintenant appliquer la démarche qui consiste à:
- 1. Quantifier le champ électrique : donc deviendra . Cette quantification va nous obliger à prendre cette fois en compte un modèle purement quantique.
- 2. Envisager que le champ se propage non plus librement, mais dans une cavité optique.
- 3. Qui dit modèle quantique dit application des postulats de la mécanique quantique.
- 4. Ainsi, l'état de ce système peut être exprimé par une surperposition linéaire des états canoniques.
- 5. Le respect de l'équation de Schrödinger permet de déterminer les coefficients intervenants dans cette superposition.
- 6. Utiliser la formule d'Euler pour écrire la fonction cosinus du champ comme combinaison linéaire de fonctions exponentielles :
- .
- 7. Exprimer l'opérateur de moment dipolaire de l'atome en fonction de ses éléments de matrice où x et y peuvent prendre les valeurs et .
- Définissons .
- Ceci permet d'écrire l'opérateur de dipole comme suit : (avec dénotant le complexe conjugué).
- L'atome ne possède pas de moment dipolaire quand il est dans un état propre d'énergie, de sorte que
Après application de l'approximation des ondes tournantes, l'hamiltonien d'interaction contient seulement deux termes. Ceux-ci correspondent à la relaxation de l'atome de son état excité vers son état fondamental avec émission simultanée d'un photon et vice versa avec absorption simultanée d'un photon lors de la transition de l'atome de son état fondamental vers son état excité.
où
- la constante représente l'intensité du couplage.
Références
- E. T. Jaynes, F. W. Cummings, « Comparison of quantum and semiclassical radiation theories with application to the beam maser », Proceedings of the IEEE, vol. 51, no 1, , p. 89–109 (DOI 10.1109/PROC.1963.1664)
- F. W. Cummings, « Stimulated emission of radiation in a single mode », Physical Review, vol. 140, no 4A, , A1051–A1056 (DOI 10.1103/PhysRev.140.A1051, Bibcode 1965PhRv..140.1051C)
- J. H. Eberly, N. B. Narozhny, and J. J. Sanchez-Mondragon, « Periodic spontaneous collapse and revival in a simple quantum model », Physical Review Letters, vol. 44, no 20, , p. 1323–1326 (DOI 10.1103/PhysRevLett.44.1323, Bibcode 1980PhRvL..44.1323E)
- G. Rempe, H. Walther, and N. Klein, « Observation of quantum collapse and revival in a one-atom maser », Physical Review Letters, vol. 58, no 4, , p. 353–356 (PMID 10034912, DOI 10.1103/PhysRevLett.58.353, Bibcode 1987PhRvL..58..353R)
- S. Haroche,, Advances in Atomic and Molecular Physics, vol. 20, New York, Academic Press, , « Radiative properties of Rydberg states in resonant cavities », p. 350
- J. A. C. Gallas, G. Leuchs, H. Walther, and H. Figger, Advances in Atomic and Molecular Physics, vol. 20, New York, Academic Press, , « Rydberg atoms: high-resolution spectroscopy and radiation interaction-Rydberg molecules », p. 414
- S. E. Morin, C. C. Yu, T. W. Mossberg, « Strong Atom-Cavity Coupling over Large Volumes and the Observation of Subnatural Intracavity Atomic Linewidths », Physical Review Letters, vol. 73, no 11, , p. 1489–1492 (PMID 10056806, DOI 10.1103/PhysRevLett.73.1489, Bibcode 1994PhRvL..73.1489M)
- T. Yoshie, A. Scherer, J. Hendrickson, G. Khitrova, H. M. Gibbs, G. Rupper, C. Ell, O. B. Shchekin & D. G. Deppe, "Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity", Nature 432, 200 (2004)
- J. Kukliński et J. Madajczyk, « Strong squeezing in the Jaynes-Cummings model », Physical Review A, vol. 37, no 8, , p. 3175–3178 (DOI 10.1103/PhysRevA.37.3175, Bibcode 1988PhRvA..37.3175K)
- J. Gea-Banacloche, « Jaynes-Cummings model with quasiclassical fields: The effect of dissipation », Physical Review A, vol. 47, no 3, , p. 2221–2234 (DOI 10.1103/PhysRevA.47.2221, Bibcode 1993PhRvA..47.2221G)
- B. Rodríguez-Lara, H. Moya-Cessa et A. Klimov, « Combining Jaynes-Cummings and anti-Jaynes-Cummings dynamics in a trapped-ion system driven by a laser », Physical Review A, vol. 71, no 2, (DOI 10.1103/PhysRevA.71.023811, Bibcode 2005PhRvA..71b3811R)
- P. Kochanski, Z. Bialynicka-Birula and I. Bialynicki-Birula, « Squeezing of electromagnetic field in a cavity by electrons in Trojan states », Physical Review A, vol. 63, , p. 013811–013811-8 (DOI 10.1103/PhysRevA.63.013811, Bibcode 2001PhRvA..63a3811K)
- A. Kundu, « Quantum Integrable Multiatom Matter-Radiation Models With and Without the Rotating-Wave Approximation », Theoretical and Mathematical Physics, vol. 144, no 1, , p. 975–984 (DOI 10.1007/s11232-005-0125-7, Bibcode 2005TMP...144..975K, arXiv nlin/0409032)
- V. Hussin et L. M. Nieto, « Ladder operators and coherent states for the Jaynes-Cummings model in the rotating-wave approximation », Journal of Mathematical Physics, vol. 46, no 12, , p. 122102 (DOI 10.1063/1.2137718, Bibcode 2005JMP....46l2102H)
- Bruce W. Shore et Peter L. Knight, « The Jaynes-Cummings Model », Journal of Modern Optics, vol. 40, no 7, , p. 1195–1238 (DOI 10.1080/09500349314551321, Bibcode 1993JMOp...40.1195S)
- D. Ellinas and I. Smyrnakis, "Asymptotics of a quantum random walk driven by an optical cavity", Journal of Optics B 7, S152 (2005).
- C. Cohen-Tannoudji, J. Dupont-Roc et G. Grynberg. Photons and Atoms. Wiley, New York, (1992).
- D. M. Meekhof, C. Monroe, W. M. Itano, B. E. King et D. J. Wineland. Generation of Non Classical Motional States of a Trapped Ion. Physical Review Letters, 76, 1796 (1996).
- J. I. Cirac, A. S. Parkins, R. Blatt et P. Zoller. Physical Review Letters, 70, 556 (1993).
- J. I. Cirac, R. Blatt, A. S. Parkins et P. Zoller. Physical Review Letters, 70, 762 (1993).

















![{\displaystyle {\hat {\sigma }}_{z}=[{\hat {\sigma }}^{+},{\hat {\sigma }}^{-}]=|e\rangle \langle e|-|f\rangle \langle f|}](https://img.franco.wiki/i/cedae6b348441d4c867853021cc3e908878fa24c.svg)

















