MD6

MD6 prend en entrée un message de taille au plus ${\displaystyle 2^{64}}$ bits, pour lequel il calcule une empreinte de d bits, où 0 < d ≤ 512 bits.

De même, un certain nombre de paramètres, possédant des valeurs par défaut, peuvent être modifiés :

• Clé K: nulle par défaut (et donc de taille 0). Peut être utilisée pour du salage.
• Hauteur de l'arbre L. En effet, comme décrit plus loin, MD6 utilise un arbre de Merkle quaternaire. Sa hauteur peut donc être spécifié. Si L vaut 0, la compression se fait selon un schéma séquentiel (de type Merkle-Damgård) permettant d'obtenir le même résultat. Si L est inférieur à 64, la compression peut être hybride, car commençant pour un parcours d'arbre pour finir pour un parcours séquentiel.
• Nombre de tour r: par défaut, ${\displaystyle \scriptstyle r=40+\lfloor d/4\rfloor }$, donc avec la valeur par défaut de d (256), r=104.
• Les autres paramètres: les constantes utilisées par la fonction de compression (Q), ou les indices des valeurs hachés à réutiliser pour le hachage du tour de boucle suivant(t1, t2, t3, t4, t5) peuvent aussi être modifié, sous certaines conditions. Par exemple, les valeurs des ti ne peuvent excéder 89.

L'arbre de Merkle de MD6

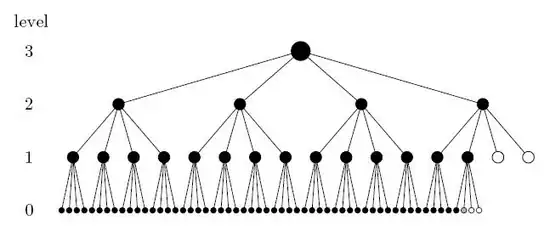
Le mode d'opération par défaut repose sur un arbre de Merkle quaternaire.

L'unité de mesure est le mot, qui vaut 8 octets, ou 64 bits.

Les feuilles de l'arbre proviennent du fichier à hacher. Elles sont éventuellement complétées par des 0 pour obtenir des feuilles de taille 16 mots, soit 128 octets ou 1024 bits. De plus, chaque nœud ayant 4 fils, des feuilles/nœuds supplémentaires composés de 0 sont ajoutés pour obtenir le bon nombre de feuilles/nœuds. Chaque bloc, composé de quatre nœuds, est compressé (avec la fonction de compression détaillée dans la partie suivante) pour obtenir en sortie un nœud de taille 16 mots.

Ainsi, on remonte dans l'arbre jusqu'à n'avoir plus qu'un seul nœud : la racine.

L'empreinte de la fonction de hachage est calculée en tronquant les d derniers bits de la racine de l'arbre (256 par défaut).

Données en entrée de la fonction de compression

La fonction de compression prend en entrée un vecteur de 89 mots, composé des éléments suivants :

• Q un vecteur de 15 mots, égal à la partie fractionnaire de ${\displaystyle \scriptstyle {\sqrt {6}}}$
• K les 8 mots de la clé (ou 0 s'il n'y a pas de clé)
• U 1 mot, indiquant la position du bloc, dont le contenu est détaillé sur la figure ci-contre
• V 1 mot, composé de r (le nombre de tour), L (la hauteur maximale de l'arbre), z (vaut 1 lors de la dernière compression, celle qui permet d'obtenir la racine, 0 sinon), p (le nombre de 0 ajouté (padding)), keylen la taille de la clé et d la taille de l'empreinte à générer
• B 1 bloc de 64 mots de données, correspondant à 4 nœuds de 16 mots

La fonction de compression, effectue ensuite r tours (par défaut 104), composé chacun de 16 boucles indépendantes. Chacune de ses 16 boucles effectue une quinzaine d'opérations logiques ou de décalage de bits (les opérations logiques sont préférées aux opérations arithmétiques et aux opérations dépendant de branchement afin d'empêcher les attaques par canaux auxiliaires).

Chaque tour calcule 89 mots, à partir des 89 mots calculés précédemment (les 89 premières valeurs sont le vecteur de 89 mots passé en entrée de la fonction de compression).

Les 64 derniers mots calculés sont la sortie de la fonction de compression.

• (en) « Papier de référence »
• (en) « Preuve de sécurité du mode d'opération de MD6 »
• (fr) « Article sur les implémentations parallèles de MD6 »