Méthode de Laplace

Illustration de la méthode de Laplace : en noir, la fonction f(x), et en rouge, e^Mf(x) avec M = 3 : on remarque que seule l'aire sous la courbe à intégrer près du maximum de ${\displaystyle f}$ (pointillés) est significative.

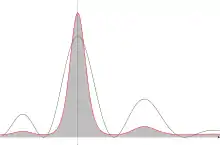
Pour M > 0, si l'on suppose que la fonction f admet un unique maximum au point ${\displaystyle x_{0}}$ alors pour M grand, seuls les points au voisinage de x₀ contribuent de façon significative à l'intégrale :

${\displaystyle \int _{a}^{b}\!\mathrm {e} ^{Mf(x)}\,\mathrm {d} x.\,}$

Si M est négatif, en considérant –M et –f on peut se ramener à considérer les maximums de –f donc les minimums de f.

Pour appliquer la méthode de Laplace, un certain nombre de conditions sont requises. Le point x₀ ne doit pas être l'une des bornes de l'intégrale et f(x) ne peut s'approcher de la valeur f(x₀) qu'au voisinage de x₀.

Par application du théorème de Taylor, au voisinage de x₀, f(x) s'écrit :

${\displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+{\frac {1}{2}}f''(x_{0})(x-x_{0})^{2}+O\left((x-x_{0})^{3}\right)}$.

Puisque f admet un maximum en x₀, qui n'est pas l'une des bornes de l'intégrale, ${\displaystyle f\,'(x_{0})=0}$ et ${\displaystyle f\,''(x_{0})<0}$, on a alors dans un voisinage de x₀ :

${\displaystyle f(x)\approx f(x_{0})-{\frac {1}{2}}|f''(x_{0})|(x-x_{0})^{2}}$

Et pour l'intégrale :

${\displaystyle \int _{a}^{b}\!\mathrm {e} ^{Mf(x)}\,\mathrm {d} x\approx \mathrm {e} ^{Mf(x_{0})}\int _{a}^{b}\!\mathrm {e} ^{-M|f''(x_{0})|(x-x_{0})^{2}/2}\,\mathrm {d} x}$

La deuxième intégrale peut être estimée à l'aide d'une intégrale de Gauss en remplaçant les bornes a et b par -∞ et +∞ et l'on a alors :

Le remplacement des bornes par -∞ et +∞ est numériquement valide car, quel que soit ${\displaystyle k\in \mathbb {N} ,\,\mathrm {e} ^{-M|f''(x_{0})|(x-x_{0})^{2}/2}}$ est un ${\displaystyle o\left((x-x_{0})^{-k}\right)}$

Les deux conditions demandées pour effectuer cette méthode ne sont pas nécessairement requises et il existe des généralisations pour le cas où x₀ est l'une des bornes en utilisant un développement au premier ordre autour de x₀ ainsi que par découpage d'intégrale pour le cas où deux, ou un nombre fini, de maximums locaux de f auraient des valeurs proches. La méthode du point col permet également une généralisation pour

${\displaystyle I(\lambda )=\int _{\mathcal {C}}f(z)\mathrm {e} ^{\lambda g(z)}\,\mathrm {d} z\,}$

La méthode de Laplace peut être employée pour démontrer la formule de Stirling :

Pour N grand :${\displaystyle N!\approx {\sqrt {2\pi N}}N^{N}\mathrm {e} ^{-N}\,}$

Par définition de la fonction gamma, on a

${\displaystyle N!=\Gamma (N+1)=\int _{0}^{\infty }\mathrm {e} ^{-x}x^{N}\,\mathrm {d} x.\,}$

Avec le changement de variable x = Nz on obtient :

${\displaystyle {\begin{aligned}N!&=\int _{0}^{\infty }\mathrm {e} ^{-Nz}\left(Nz\right)^{N}N\,\mathrm {d} z=N^{N+1}\int _{0}^{\infty }\mathrm {e} ^{-Nz}z^{N}\,\mathrm {d} z\\&=N^{N+1}\int _{0}^{\infty }\mathrm {e} ^{-Nz}\mathrm {e} ^{N\ln z}\,\mathrm {d} z=N^{N+1}\int _{0}^{\infty }\mathrm {e} ^{N(\ln z-z)}\,\mathrm {d} z.\end{aligned}}}$

En considérant la fonction f(z) = ln(z) – z, qui est deux fois dérivable :

${\displaystyle f'(z)={\frac {1}{z}}-1\,,\ f''(z)=-{\frac {1}{z^{2}}}.\,}$

on voit que f atteint son maximum en z = 1 et sa dérivée seconde vaut –1 en 1 ; on a alors avec la méthode de Laplace :

${\displaystyle N!\approx N^{N+1}{\sqrt {\frac {2\pi }{N}}}\mathrm {e} ^{-N}={\sqrt {2\pi N}}N^{N}\mathrm {e} ^{-N}.\,}$