Loi de Koomey
La loi de Koomey décrit une tendance à long terme dans l'histoire des ordinateurs. Selon cette loi, le nombre de calculs par joule (unité d'énergie) dépensé double tous les 18 mois environ. Il s'avère que cette tendance a été remarquablement stable depuis les années 1950, le nombre de calculs par joule dépensé ayant doublé environ tous les 1,57 ans. Cette loi énoncée par Jonathan Koomey aurait été énoncée comme suit : la quantité d'énergie dont une machine a besoin pour effectuer un nombre donné de calculs va diminuer d'un facteur deux chaque année et demi[1].
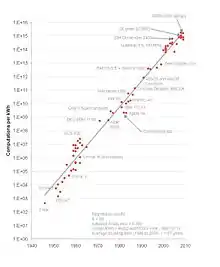
« The idea is that at a fixed computing load, the amount of battery you need will fall by a factor of two every year and a half. »[2]
Elle établit un parallèle avec la loi de Moore[3].
Limitations
L'une des limitations les plus connues à cette loi est la limite de Landauer proposée par le physicien Rolf Landauer. Le principe de Landauer affirme que tout calcul produit une augmentation d'entropie si ce calcul est irréversible. De cette augmentation d'entropie résulte une perte d'énergie qui se manifeste par un dégagement de chaleur[4]. Cette limite peut être contournée par l'usage du calcul réversible.
En 1973, Charles Bennett montra qu'il était possible de concevoir des machines à calculer générales logiquement et thermodynamiquement réversibles. De ce résultat, il s'ensuit que tout calcul peut être réalisé physiquement de manière réversible[5] - [6].
Le théorème de Margolus-Levitin constitue une autre limitation à la loi de Koomey. Ce théorème, dû à Norman Margolus et Lev Berovich Levitin (en), établit une limite fondamentale au calcul quantique qui ne peut dépasser le nombre de 6 × 1033 opérations par seconde et par joule (unité d'énergie)[7]. Autrement dit, pour l'utilisation d'un joule, il serait possible à une machine de réaliser jusqu'à 6 000 000 000 000 000 000 000 000 000 000 000 (6 millions de milliards de milliards de milliards) d'opérations par seconde mais pas davantage. La puissance des superordinateurs existants nous place très loin de cette limite[8].
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Koomey's law » (voir la liste des auteurs).
- « New 'Koomey’s Law' of power efficiency parallels Moore'e Law », Phys.org.
- « A New and Improved Moore's Law », MIT Technology review
- (en) Koomey, Jonathan; Berard, Stephen; Sanchez, Marla; Wong, Henry;, « Implications of Historical Trends in the Electrical Efficiency of Computing », IEEE Annals of the History of Computing, vol. 33, no 3, , p. 46–54 (ISSN 1058-6180, DOI 10.1109/MAHC.2010.28, lire en ligne)
- (en) Rolf Landauer, « Irreversibility and heat generation in the computing process », IBM Journal of Research and Development, vol. 5, no 3, , p. 183-191 (DOI 10.1147/rd.53.0183, lire en ligne, consulté le )
- « Logical Reversibility of Computation », C. H. Bennett, IBM Journal of Research and Development 17:525-532 (November, 1973)
- « Reversible computing » Charles Bennett (1973) (IBM) first showed how any computation could be embedded in an equivalent reversible computation, CHAPTER II. PHYSICS OF COMPUTATION
- (en) Norman Margolus, Lev B. Levitin, « The maximum speed of dynamical evolution », Physica D, vol. 120, , p. 188–195 (DOI 10.1016/S0167-2789(98)00054-2, Bibcode 1998PhyD..120..188M, arXiv quant-ph/9710043)
- (en) Seth Lloyd, « Ultimate physical limits to computation », Nature, vol. 406, no 6799, , p. 1047–1054 (ISSN 0028-0836, DOI 10.1038/35023282, lire en ligne, consulté le )