Loi de Bates
En théorie des probabilités et en statistique, la loi de Bates, dénommée suivant la probabiliste Grace E. Bates, est la loi de probabilité de la moyenne de variables aléatoires indépendantes et de loi uniforme continue sur [0 ; 1][1].
| Loi de Bates | |
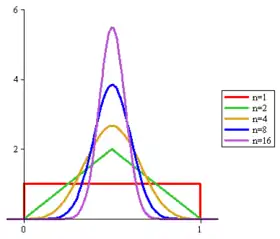 Densité de probabilité | |
| Paramètres | n >1 réel |
|---|---|
| Support | |
| Densité de probabilité | pour |
| Espérance | |
| Variance | |
| Asymétrie | 0 |
| Kurtosis normalisé | |
| Fonction caractéristique | |
Il ne faut pas confondre cette loi avec la loi d'Irwin-Hall qui est la somme de telles variables aléatoires.
Définition
La loi de Bates est la loi de probabilité de la moyenne arithmétique de n variables aléatoires U1, U2, ... , Un iid de loi uniforme continue sur l'intervalle [0 ; 1] :
La densité de probabilité de la loi de Bates est donnée par la formule suivante[2] :
Plus généralement, la moyenne de n variables aléatoires indépendantes et uniformes sur [a , b] :
a pour densité de probabilité
Notes et références
- (en) N. Balakrishnan, N.L. Jonhson et S. Kotz, Continuous Univariate Distributions, vol. 2, Wiley, , 2e éd. (ISBN 0-471-58494-0), section 26.9
- (en) Grace E. Bates, « Joint Distributions of Time Intervals for the Occurrence of Successive Accidents in a Generalized Polya Scheme », Annal of Mathematical Statistics, vol. 26, no 4, , p. 705-720 (lire en ligne)
Voir aussi
Lien externe
- « (en) BatesDistribution », sur Wolfram Mathematica-Documentation center (consulté le )
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.

![{\displaystyle x\in [a,b]}](https://img.franco.wiki/i/026357b404ee584c475579fb2302a4e9881b8cce.svg)

![{\displaystyle x\in ]0;1[}](https://img.franco.wiki/i/76385da4fca47c44a1f3590201404d819f0b4d29.svg)



![{\displaystyle \left[-{\frac {\mathrm {i} n\left(\mathrm {e} ^{\tfrac {ibt}{n}}-\mathrm {e} ^{\tfrac {\mathrm {i} at}{n}}\right)}{(b-a)t}}\right]^{n}}](https://img.franco.wiki/i/eeeb117cd01a918edd18110c4221f99e5f1223cc.svg)

![{\displaystyle f_{X}(x;n)={\begin{cases}\displaystyle {\frac {n^{n}}{\left(n-1\right)!}}\sum _{k=0}^{\lfloor nx\rfloor }\left(-1\right)^{k}{n \choose k}\left(x-{\frac {k}{n}}\right)^{n-1}&{\text{ pour }}x\in ]0,1[\\0&{\text{sinon.}}\end{cases}}}](https://img.franco.wiki/i/a40751ea1dead89d8ec82201bee01e4444a12fe0.svg)

