Loi d'Erlang
La distribution d'Erlang est une loi de probabilité continue, dont l'intérêt est dû à sa relation avec les distributions exponentielle et Gamma. Cette distribution a été développée par Agner Krarup Erlang afin de modéliser le nombre d'appels téléphoniques simultanés.
| Erlang | |
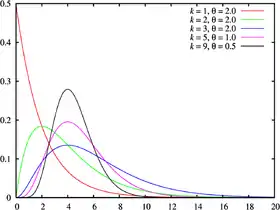 Densité de probabilité Graphes de densités pour la distribution d'Erlang. | |
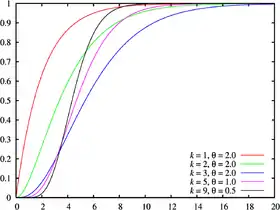 Fonction de répartition Graphes de fonctions de répartition pour la distribution d'Erlang. | |
| Paramètres | Paramètre de forme (entier) intensité (réel) alt.: paramètre d'échelle (réel) |
|---|---|
| Support | |
| Densité de probabilité | |
| Fonction de répartition | |
| Espérance | |
| Médiane | pas de forme simple |
| Mode | pour |
| Variance | |
| Asymétrie | |
| Kurtosis normalisé | |
| Entropie | |
| Fonction génératrice des moments | pour |
| Fonction caractéristique | |
Généralité
La distribution est continue et possède deux paramètres: le paramètre de forme , un entier, et le paramètre d'intensité , un réel. On utilise parfois une paramétrisation alternative, où on considère plutôt le paramètre d'échelle .
Lorsque le paramètre de forme vaut 1, la distribution se simplifie en la loi exponentielle.
La distribution d'Erlang est un cas spécial de la loi Gamma, où le paramètre de forme est un entier. Dans la loi Gamma, ce paramètre est réel positif supérieur ou égal à 1.
Caractérisation
Densité de probabilité
La densité de probabilité de la distribution d'Erlang est
Le paramètre est le paramètre de forme, et le paramètre d'intensité. Une paramétrisation équivalente met en jeu le paramètre d'échelle , défini comme l'inverse de l'intensité (c'est-à-dire ):
La présence de la factorielle implique que k doit être un entier naturel supérieur ou égal à 1.
Fonction de répartition
La fonction de répartition de la distribution d'Erlang est
où est la fonction gamma incomplète. Cette fonction peut aussi s'écrire :
Occurrences
Processus de renouvellement
La distribution d'Erlang est la distribution de la somme de k variables aléatoires indépendantes et identiquement distribuées selon une loi exponentielle de paramètre . Si chacune de ces variables aléatoires représente le temps au bout duquel un événement donné se produit (par exemple, une intervention à la suite d'une panne sur un appareil sans usure et sans mémoire), alors la variable aléatoire au bout duquel le k-ème événement a lieu suit une loi d'Erlang de forme k et de paramètre .
Processus de Poisson
Si l'on se donne un instant t, on montre que la variable aléatoire égale au nombre d'entiers k tels que suit une loi de Poisson de paramètre [1]. Dans l'interprétation ci-dessus, est le nombre d'interventions effectuées avant l'instant t.
Voir aussi
- Processus de Poisson
- Loi binomiale négative : cette loi est l'analogue de la loi d'Erlang dans le cas discret.
Liens externes
Références
- Didier Dacunha-Castelle, Marie Duflo, Probabilités et statistiques, T.1, problèmes à temps fixe, Masson (1982)






























