Liste de nombres premiers

Aucune liste de nombres premiers finie ne peut être exhaustive car il existe une infinité de nombres premiers. On ne connaît d’ailleurs pas non plus de formule simple produisant une telle liste.

Des listes plus longues de nombres premiers sont disponibles, notamment sur les sites de :

l'encyclopédie en ligne des suites de nombres entiers (OEIS)[1] ;
l'université d'Utah (U)[2] ;
l'université du Tennessee at Martin (UTM)[3] ;
l'université d'Arizona (Chris Caldwell)[4] ;
Gérard Villemin[5].

Les 1 000 premiers nombres premiers

Les paires de nombres premiers jumeaux sont en gras. Les paires de paires (ou quadruplets), séparées seulement par 4 unités, et beaucoup plus rares, sont en gras souligné. Ces quadruplets, comme les simples paires, sont heuristiquement en nombre infini, comme l'affirme (de façon quantitativement plus précise) la conjecture de Bateman-Horn.

Rang	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1–20	2	3	5	7	11	13	17	19	23	29	31	37	41	43	47	53	59	61	67	71
21–40	73	79	83	89	97	101	103	107	109	113	127	131	137	139	149	151	157	163	167	173
41–60	179	181	191	193	197	199	211	223	227	229	233	239	241	251	257	263	269	271	277	281
61–80	283	293	307	311	313	317	331	337	347	349	353	359	367	373	379	383	389	397	401	409
81–100	419	421	431	433	439	443	449	457	461	463	467	479	487	491	499	503	509	521	523	541
101–120	547	557	563	569	571	577	587	593	599	601	607	613	617	619	631	641	643	647	653	659
121–140	661	673	677	683	691	701	709	719	727	733	739	743	751	757	761	769	773	787	797	809
141–160	811	821	823	827	829	839	853	857	859	863	877	881	883	887	907	911	919	929	937	941
161–180	947	953	967	971	977	983	991	997	1 009	1 013	1 019	1 021	1 031	1 033	1 039	1 049	1 051	1 061	1 063	1 069
181–200	1 087	1 091	1 093	1 097	1 103	1 109	1 117	1 123	1 129	1 151	1 153	1 163	1 171	1 181	1 187	1 193	1 201	1 213	1 217	1 223
201–220	1 229	1 231	1 237	1 249	1 259	1 277	1 279	1 283	1 289	1 291	1 297	1 301	1 303	1 307	1 319	1 321	1 327	1 361	1 367	1 373
221–240	1 381	1 399	1 409	1 423	1 427	1 429	1 433	1 439	1 447	1 451	1 453	1 459	1 471	1 481	1 483	1 487	1 489	1 493	1 499	1 511
241–260	1 523	1 531	1 543	1 549	1 553	1 559	1 567	1 571	1 579	1 583	1 597	1 601	1 607	1 609	1 613	1 619	1 621	1 627	1 637	1 657
261–280	1 663	1 667	1 669	1 693	1 697	1 699	1 709	1 721	1 723	1 733	1 741	1 747	1 753	1 759	1 777	1 783	1 787	1 789	1 801	1 811
281–300	1 823	1 831	1 847	1 861	1 867	1 871	1 873	1 877	1 879	1 889	1 901	1 907	1 913	1 931	1 933	1 949	1 951	1 973	1 979	1 987
301–320	1 993	1 997	1 999	2 003	2 011	2 017	2 027	2 029	2 039	2 053	2 063	2 069	2 081	2 083	2 087	2 089	2 099	2 111	2 113	2 129
321–340	2 131	2 137	2 141	2 143	2 153	2 161	2 179	2 203	2 207	2 213	2 221	2 237	2 239	2 243	2 251	2 267	2 269	2 273	2 281	2 287
341–360	2 293	2 297	2 309	2 311	2 333	2 339	2 341	2 347	2 351	2 357	2 371	2 377	2 381	2 383	2 389	2 393	2 399	2 411	2 417	2 423
361–380	2 437	2 441	2 447	2 459	2 467	2 473	2 477	2 503	2 521	2 531	2 539	2 543	2 549	2 551	2 557	2 579	2 591	2 593	2 609	2 617
381–400	2 621	2 633	2 647	2 657	2 659	2 663	2 671	2 677	2 683	2 687	2 689	2 693	2 699	2 707	2 711	2 713	2 719	2 729	2 731	2 741
401–420	2 749	2 753	2 767	2 777	2 789	2 791	2 797	2 801	2 803	2 819	2 833	2 837	2 843	2 851	2 857	2 861	2 879	2 887	2 897	2 903
421–440	2 909	2 917	2 927	2 939	2 953	2 957	2 963	2 969	2 971	2 999	3 001	3 011	3 019	3 023	3 037	3 041	3 049	3 061	3 067	3 079
441–460	3 083	3 089	3 109	3 119	3 121	3 137	3 163	3 167	3 169	3 181	3 187	3 191	3 203	3 209	3 217	3 221	3 229	3 251	3 253	3 257
461–480	3 259	3 271	3 299	3 301	3 307	3 313	3 319	3 323	3 329	3 331	3 343	3 347	3 359	3 361	3 371	3 373	3 389	3 391	3 407	3 413
481–500	3 433	3 449	3 457	3 461	3 463	3 467	3 469	3 491	3 499	3 511	3 517	3 527	3 529	3 533	3 539	3 541	3 547	3 557	3 559	3 571
501–520	3 581	3 583	3 593	3 607	3 613	3 617	3 623	3 631	3 637	3 643	3 659	3 671	3 673	3 677	3 691	3 697	3 701	3 709	3 719	3 727
521–540	3 733	3 739	3 761	3 767	3 769	3 779	3 793	3 797	3 803	3 821	3 823	3 833	3 847	3 851	3 853	3 863	3 877	3 881	3 889	3 907
541–560	3 911	3 917	3 919	3 923	3 929	3 931	3 943	3 947	3 967	3 989	4 001	4 003	4 007	4 013	4 019	4 021	4 027	4 049	4 051	4 057
561–580	4 073	4 079	4 091	4 093	4 099	4 111	4 127	4 129	4 133	4 139	4 153	4 157	4 159	4 177	4 201	4 211	4 217	4 219	4 229	4 231
581–600	4 241	4 243	4 253	4 259	4 261	4 271	4 273	4 283	4 289	4 297	4 327	4 337	4 339	4 349	4 357	4 363	4 373	4 391	4 397	4 409
601–620	4 421	4 423	4 441	4 447	4 451	4 457	4 463	4 481	4 483	4 493	4 507	4 513	4 517	4 519	4 523	4 547	4 549	4 561	4 567	4 583
621–640	4 591	4 597	4 603	4 621	4 637	4 639	4 643	4 649	4 651	4 657	4 663	4 673	4 679	4 691	4 703	4 721	4 723	4 729	4 733	4 751
641–660	4 759	4 783	4 787	4 789	4 793	4 799	4 801	4 813	4 817	4 831	4 861	4 871	4 877	4 889	4 903	4 909	4 919	4 931	4 933	4 937
661–680	4 943	4 951	4 957	4 967	4 969	4 973	4 987	4 993	4 999	5 003	5 009	5 011	5 021	5 023	5 039	5 051	5 059	5 077	5 081	5 087
681–700	5 099	5 101	5 107	5 113	5 119	5 147	5 153	5 167	5 171	5 179	5 189	5 197	5 209	5 227	5 231	5 233	5 237	5 261	5 273	5 279
701–720	5 281	5 297	5 303	5 309	5 323	5 333	5 347	5 351	5 381	5 387	5 393	5 399	5 407	5 413	5 417	5 419	5 431	5 437	5 441	5 443
721–740	5 449	5 471	5 477	5 479	5 483	5 501	5 503	5 507	5 519	5 521	5 527	5 531	5 557	5 563	5 569	5 573	5 581	5 591	5 623	5 639
741–760	5 641	5 647	5 651	5 653	5 657	5 659	5 669	5 683	5 689	5 693	5 701	5 711	5 717	5 737	5 741	5 743	5 749	5 779	5 783	5 791
761–780	5 801	5 807	5 813	5 821	5 827	5 839	5 843	5 849	5 851	5 857	5 861	5 867	5 869	5 879	5 881	5 897	5 903	5 923	5 927	5 939
781–800	5 953	5 981	5 987	6 007	6 011	6 029	6 037	6 043	6 047	6 053	6 067	6 073	6 079	6 089	6 091	6 101	6 113	6 121	6 131	6 133
801–820	6 143	6 151	6 163	6 173	6 197	6 199	6 203	6 211	6 217	6 221	6 229	6 247	6 257	6 263	6 269	6 271	6 277	6 287	6 299	6 301
821–840	6 311	6 317	6 323	6 329	6 337	6 343	6 353	6 359	6 361	6 367	6 373	6 379	6 389	6 397	6 421	6 427	6 449	6 451	6 469	6 473
841–860	6 481	6 491	6 521	6 529	6 547	6 551	6 553	6 563	6 569	6 571	6 577	6 581	6 599	6 607	6 619	6 637	6 653	6 659	6 661	6 673
861–880	6 679	6 689	6 691	6 701	6 703	6 709	6 719	6 733	6 737	6 761	6 763	6 779	6 781	6 791	6 793	6 803	6 823	6 827	6 829	6 833
881–900	6 841	6 857	6 863	6 869	6 871	6 883	6 899	6 907	6 911	6 917	6 947	6 949	6 959	6 961	6 967	6 971	6 977	6 983	6 991	6 997
901–920	7 001	7 013	7 019	7 027	7 039	7 043	7 057	7 069	7 079	7 103	7 109	7 121	7 127	7 129	7 151	7 159	7 177	7 187	7 193	7 207
921–940	7 211	7 213	7 219	7 229	7 237	7 243	7 247	7 253	7 283	7 297	7 307	7 309	7 321	7 331	7 333	7 349	7 351	7 369	7 393	7 411
941–960	7 417	7 433	7 451	7 457	7 459	7 477	7 481	7 487	7 489	7 499	7 507	7 517	7 523	7 529	7 537	7 541	7 547	7 549	7 559	7 561
961–980	7 573	7 577	7 583	7 589	7 591	7 603	7 607	7 621	7 639	7 643	7 649	7 669	7 673	7 681	7 687	7 691	7 699	7 703	7 717	7 723
981–1000	7 727	7 741	7 753	7 757	7 759	7 789	7 793	7 817	7 823	7 829	7 841	7 853	7 867	7 873	7 877	7 879	7 883	7 901	7 907	7 919

Suites remarquables de nombres premiers

De nombreuses suites de nombres premiers possèdent des propriétés remarquables[6]. Par exemple, les nombres premiers jumeaux (tels 3 et 5) ou les nombres de Mersenne premiers tels que 7 ou 31 (et dont sont notamment issus les plus grands nombres premiers connus).

Répartition des nombres premiers

Répartition des nombres premiers jusqu'à 1 000 000:

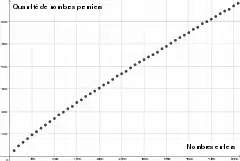
Quantité cumulée de nombres premiers par centaines d'entiers naturels.

4 nombres premiers sont inférieurs à 10,
25 nombres premiers sont inférieurs à 100,
168 nombres premiers sont inférieurs à 1 000,
1 229 nombres premiers sont inférieurs à 10 000,
9 592 nombres premiers sont inférieurs à 100 000,
17 984 nombres premiers sont inférieurs à 200 000,
25 997 nombres premiers sont inférieurs à 300 000,
33 860 nombres premiers sont inférieurs à 400 000,
41 538 nombres premiers sont inférieurs à 500 000,
49 098 nombres premiers sont inférieurs à 600 000,
56 543 nombres premiers sont inférieurs à 700 000,
63 951 nombres premiers sont inférieurs à 800 000,
71 274 nombres premiers sont inférieurs à 900 000,
78 498 nombres premiers sont inférieurs à 1 000 000.

Plus généralement, l'étude de la répartition des nombres premiers, en particulier le théorème des nombres premiers, montre que la proportion des nombres premiers compris entre $0$ (zéro) et une borne supérieure $x$ (entière ou réelle) diminue, pour tendre vers 0 comme l'inverse du logarithme $1/\ln(x)$ (soit très lentement), lorsque $x$ tend vers +∞.

Notes et références

Suite A000040 : the prime numbers.
(en) math.utah.edu The University of Utah : The 1,000 smallest prime numbers.
(en) primes.utm.edu The first fifty million primes (Chris Caldwell).
(en)cs.arizona.edu The University of Arizona : List of 50000 Primes.
villemin.gerard.free.fr Nombres premiers : Listes et tables.
(en) mathworld.wolfram.com MathWorld : Integer Sequence Primes.

Voir aussi

Liens externes

(en) www.rsok.com « Some Prime Numbers » (Interface vers une liste des premiers 98 millions de nombres premiers, inférieurs à 8 000 000 000)
(en) www.bigprimes.net « Bigprimes.net » (Les 1 milliard 400 millions premiers nombres premiers)
(en) mathworld.wolfram.com « MathWorld » : Number Theory > Prime Numbers > Prime Number Sequences
nombrespremiersliste.free.fr « Les nombres premiers » (Liste simple des nombres premiers jusqu'à 1 000 000 000)

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.