Jeu d'Ehrenfeucht-Fraïssé

Deux structures. La première est un graphe à 4 éléments (un carré). La seconde, à 6 éléments, est deux carrés adjacents.

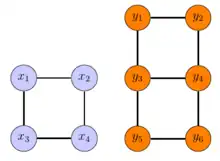
Le jeu d'Ehrenfeucht-Fraïssé se joue sur deux structures et entre deux joueurs appelés spoiler et duplicateur. La figure ci-contre montre deux structures. Le spoiler veut montrer que les deux structures sont différentes, alors que le duplicateur veut montrer qu'elles sont isomorphes. Le jeu est joué en un nombre fini de tours. Un tour se déroule comme suit : d'abord, le spoiler choisit un élément arbitraire de l'une des deux structures, et ensuite le duplicateur choisit un élément de l'autre structure. La tâche du duplicateur est de toujours choisir un élément qui est « similaire » à celui choisi par le spoiler. Par exemple, si le spoiler choisit x₁, le duplicateur est tenté de répondre par y₁, y₂, y₆ ou y₅, mais a priori pas y3 (et y4) car y3 ne ressemble pas à un coin de carré.

Lorsque tous les tours sont joués, le duplicateur gagne si les éléments choisis dans la première structure forment une structure isomorphe à la restriction aux éléments choisis dans la seconde. Par exemple, si on joue deux tours, voici deux exemples de parties du jeu :

• le spoiler choisit x₁, le duplicateur répond par y₁, le spoiler choisit y₄, le duplicateur répond par x₄. Les éléments choisis dans la première structure sont déconnectés (il n'y a pas d'arête entre x₁ et x₄), de même pour ceux de la seconde structure. Le duplicateur gagne.
• le spoiler choisit x₁, le duplicateur répond par y₁, le spoiler choisit x₂, le duplicateur répond par y₃. Les éléments choisis dans la première structure sont connectés (il y a une arête entre x₁ et x₂), de même pour ceux de la seconde structure. Le duplicateur gagne.
• le spoiler choisit x₁, le duplicateur répond par y₁, le spoiler choisit x₂, le duplicateur répond par y₄. Les éléments choisis dans la première structure sont connectés (il y a une arête entre x₁ et x₂), mais pas dans la seconde structure. Le duplicateur a mal joué et perd.

On suppose données deux structures ${\displaystyle A}$ et ${\displaystyle B}$, sans symboles de fonction et avec le même ensemble de symboles de relation. On fixe un entier naturel n. Le jeu d'Ehrenfeucht-Fraïssé ${\displaystyle G_{n}(A,B)}$ entre deux joueurs, le spoiler et le duplicateur, se joue comme suit :

1. Le spoiler joue en premier et choisit un élément ${\displaystyle a_{1}}$ de ${\displaystyle A}$ ou un élément ${\displaystyle b_{1}}$ de ${\displaystyle B}$.
2. Si le spoiler a pris un élément de ${\displaystyle A}$, le duplicateur choisit un élément ${\displaystyle b_{1}}$ de ${\displaystyle B}$; sinon, le duplicateur choisit un élément ${\displaystyle a_{1}}$ de ${\displaystyle A}$.
3. Le spoiler choisit un élément ${\displaystyle a_{2}}$ de ${\displaystyle A}$ ou un élément ${\displaystyle b_{2}}$ de ${\displaystyle B}$.
4. Le duplicateur choisit un élément ${\displaystyle a_{2}}$ ou ${\displaystyle b_{2}}$ dans la structure que le spoiler n'a pas choisie.
5. Le spoiler et le duplicateur continuent de choisir des éléments dans ${\displaystyle A}$ et ${\displaystyle B}$ jusqu'à obtenir ${\displaystyle n}$ éléments chacun.
6. À la fin du jeu, des éléments ${\displaystyle a_{1},\dots ,a_{n}}$ de ${\displaystyle A}$ et ${\displaystyle b_{1},\dots ,b_{n}}$ de ${\displaystyle B}$ ont été choisis. Le duplicateur gagne le jeu si l'application ${\displaystyle a_{i}\to b_{i}}$ est un isomorphisme partiel, et sinon c'est le spoiler qui gagne.

Pour chaque entier n, on définit la relation ${\displaystyle A\sim _{n}B}$ par la propriété que le duplicateur gagne le jeu ${\displaystyle G_{n}(A,B)}$ à n tours. Il est facile de prouver que si le duplicateur gagne pour tout n, alors ${\displaystyle A}$ et ${\displaystyle B}$ sont élémentairement équivalent. Si l'ensemble des symboles de relations est fini, la réciproque est également vraie.

L'importance du jeu réside dans le fait que ${\displaystyle A\sim _{n}B}$ si et seulement si ${\displaystyle A}$ et ${\displaystyle B}$ satisfont les mêmes formules du premier ordre de rang de quantificateurs au plus ${\displaystyle n}$. Ceci fournit un outil efficace[1] pour prouver qu'une propriété ${\displaystyle P}$ n'est pas définissable en logique du premier ordre. Pour cela, on cherche deux familles ${\displaystyle A_{n}}$ et ${\displaystyle B_{n}}$ de structures telles que toutes les ${\displaystyle A_{n}}$ vérifient ${\displaystyle P}$ et aucune des ${\displaystyle B_{n}}$ ne la vérifie, et que ${\displaystyle A_{n}\sim _{n}B_{n}}$. Si on suppose que ${\displaystyle P}$ est exprimable par une formule de rang de quantificateurs au plus ${\displaystyle n}$ et que ${\displaystyle A_{n}}$ la vérifie, la structure ${\displaystyle B_{n}}$ ne la vérifie pas, en contradiction avec les faits que ${\displaystyle A_{n}\sim _{n}B_{n}}$.

La méthode du va-et-vient utilisée dans le jeu d'Ehrenfeucht-Fraïssé pour vérifier l'équivalence élémentaire a été formulée par Roland Fraïssé dans une note aux Comptes rendus de l'Académie des sciences[2] et dans sa thèse[3]. Elle a été exprimée comme un jeu par Andrzej Ehrenfeucht[4]. Les noms de « spoiler » et « duplicateur » sont dus à Joel Spencer[5]. D'autres noms employés sont Éloise et Abélard (et souvent notés ∃ et ∀) d'après Héloïse et Abélard, une dénomination introduite par Wilfrid Hodges dans son livre Model Theory. Neil Immerman suggère « Samson » et « Delilah », avec les mêmes initiales. Le problème de décider si le duplicateur gagne à un jeu de Ehrenfeucht-Fraïssé est PSPACE-complet[6].

On peut définir des variantes aux jeux d'Ehrenfeucht-Fraïssé pour caractériser la définissabilité dans d'autres logiques.

Le jeu d'Ehrenfeucht-Fraïssé est exposé dans de nombreux manuels de référence, parmi lesquels il y a les suivants :

• (en) Joseph G. Rosenstein, Linear Orderings, New York, Academic Press, 1982, 487 p. (ISBN 978-0-12-597680-0).

• Bruno Poizat, A Course in Model Theory : An Introduction to Contemporary Mathematical Logic, Springer, coll. « Universitext », 2000, 443 p. (ISBN 978-1-4612-6446-0).
• (en) Neil Immerman, Descriptive Complexity, New York, Springer, 1999, 268 p. (ISBN 0-387-98600-6, lire en ligne) — Chapitre 6
• (en) Wilfrid Hodges, Model theory, Cambridge, Cambridge University Press, 2008, 788 p. (ISBN 978-0-521-06636-5, OCLC 219990733)
• (en) Erich Grädel, Phokion G. Kolaitis, Leonid Libkin, Marx Maarten, Joel Spencer, Moshe Y. Vardi, Yde Venema et Scott Weinstein, Finite model theory and its applications, Berlin, Springer-Verlag, coll. « Texts in Theoretical Computer Science. An EATCS Series », 2007, 437 p. (ISBN 978-3-540-00428-8, zbMATH 1133.03001, lire en ligne)
• Leonid Libkin, « Elements of Finite Model Theory — Introduction »

• Un exemple consultable en ligne : Ivars Peterson, « Example of the Ehrenfeucht-Fraïssé game », MathTrek
• Six Lectures Ehrenfeucht-Fraïssé games at MATH EXPLORERS' CLUB, Cornell Department of Mathematics.