Intégrale de Jacobi
En mécanique céleste, l'intégrale de Jacobi ou constante de Jacobi (d'après Charles Gustave Jacob Jacobi) est la seule quantité conservée dans le problème à trois corps restreint circulaire[1] ; contrairement au cas du problème à deux corps, l'énergie et le moment cinétique du système ne sont pas conservés séparément et une solution analytique générale n'est pas possible. Cette intégrale a été utilisée pour fournir des solutions à des cas particuliers du problème à trois corps.
Définition
Système de coordonnées synodique
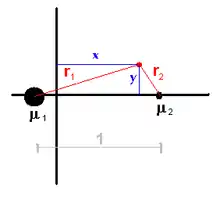
Le système de coordonnées utilisé est appelé synodique ou système co-rotationnel, placé au barycentre, la ligne connectant les deux masses μ1, μ2 étant choisie comme l'axe x et la longueur unité égale à leur distance. Comme le système tourne en même temps que les deux masses, celles-ci restent stationnaires et positionnées à (−μ2, 0) et à (+μ1, 0)1.
Dans le système de coordonnées (x, y), l'intégrale de Jacobi s'exprime comme :
où :
- est le mouvement moyen (T est la période orbitale)
- , pour les masses m1, m2 et G est la constante gravitationnelle
- sont les distances de la particule test aux deux masses
On notera que l'intégrale de Jacobi vaut moins deux fois l'énergie totale par unité de masse dans le référentiel de référence tournant : le premier terme représente l'énergie potentielle centrifuge, le second représente l'énergie potentielle gravitationnelle et le troisième est l'énergie cinétique. Dans ce système de référence, les forces qui agissent sur la particule sont les deux attractions gravitationnelles, la force centrifuge et la force de Coriolis. Puisque les trois premières dérivent de potentiels et que la dernière est perpendiculaire à la trajectoire, elles sont toutes conservatives, et donc l'énergie calculée dans ce système de référence (et donc l'intégrale de Jacobi) est une constante du mouvement. Une preuve calculatoire directe est donnée ci-dessous.
Système de coordonnées sidéral
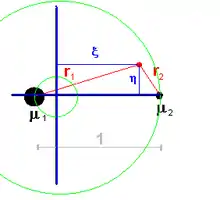
Dans le système de coordonnées sidéral inertiel (ξ, η, ζ), les masses orbitent autour du barycentre. Dans ce système de coordonnées, l'intégrale de Jacobi s'exprime par :
Démonstration
Dans le système co-rotationnel, les accélérations peuvent être exprimées comme les dérivées d'une simple fonction scalaire
En utilisant une représentation lagrangienne des équations du mouvement :
[Eq.1]
[Eq.2]
[Eq.3]
En multipliant respectivement les [Eq.1], [Eq.2] et [Eq.3] par et et en les additionnant, on obtient
L'intégration fournit
où CJ est la constante d'intégration.
Le terme de gauche représente le carré de la vitesse v de la particule test dans le système co-rotationnel.
1Ce système de coordonnées est non inertiel, ce qui explique l'apparition de termes relatifs aux accélérations centrifuge et de Coriolis.
Voir aussi
Références
- Carl Gustav Jacob Jacobi, « Sur le movement d'un point et sur un cas particulier du problème des trois corps », Comptes Rendus de l'Académie des Sciences de Paris, vol. 3, , p. 59–61 (lire en ligne)
- Carl D. Murray and Stanley F. Dermot Solar System Dynamics [Cambridge, England: Cambridge University Press, 1999], pages 68–71. (ISBN 0-521-57597-4)
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Jacobi integral » (voir la liste des auteurs).












