Indice de Theil

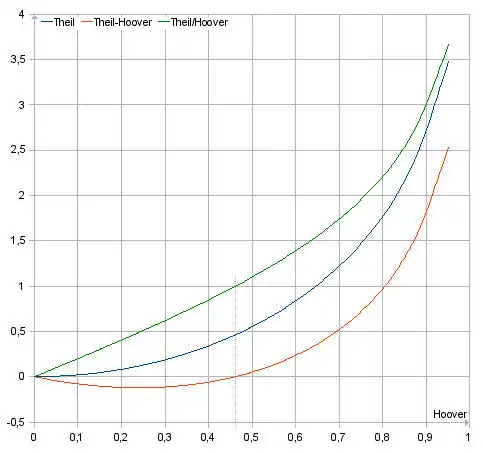
Illustration de la relation entre l'indice de Theil T et l'indice de Hoover H (différence T-H et quotient T/H) pour des sociétés divisées en deux quantiles, ou A % des peuples ont B % des ressources et B % des peuples ont A % de toutes les ressources. A+B=100 %. Pour de telles sociétés, l'indice de Hoover et le coefficient de Gini sont les mêmes mesures. ${\displaystyle T=T_{T}=T_{L}=T_{s}=2H\,\operatorname {argtanh} \left(H\right)\,}$

Formule[2] pour l'indice de Theil ${\displaystyle \displaystyle {}T}$ :

• ${\displaystyle N}$ : nombre des quantiles,
• ${\displaystyle E_{i}}$ : ressources pour le quantile i,
• ${\displaystyle A_{i}}$ : effectif dans le quantile i,
• ${\displaystyle E_{\mathrm {total} }}$ : ressources pour tous les quantiles dans une société (une nation, etc.),
• ${\displaystyle A_{\mathrm {total} }}$ : effectif de la société (de la nation, etc.).

${\displaystyle T_{T}=\ln {\frac {{A}_{\mathrm {total} }}{{E}_{\mathrm {total} }}}-{\frac {\sum _{i=1}^{N}{{E}_{i}}\ln {\frac {{A}_{i}}{{E}_{i}}}}{{E}_{\mathrm {total} }}}}$

En cas de ${\displaystyle {{E}'_{i}}=E_{i}/E_{\text{total}}}$ et ${\displaystyle {{A}'_{i}}=A_{i}/A_{\text{total}}}$:
${\displaystyle \color {Gray}T_{T}=0-{\frac {\sum _{i=1}^{N}{{E}'_{i}}\ln {\frac {{A}'_{i}}{{E}'_{i}}}}{1}}=\sum _{i=1}^{N}{{E}'_{i}}\ln {\frac {{E}'_{i}}{{A}'_{i}}}}$

C'est l'inégalité par référence aux ressources. La partie à gauche est l'entropie maximale (aussi par référence aux ressources) d'une société sans inégalité distributive. La partie à droite est l'entropie réelle de la société, causée par l'inégalité distributive de cette société. Par référence à la théorie de l'information[3], une telle différence est la redondance.

L'inégalité par référence à la population :

${\displaystyle T_{L}=\ln {\frac {{E}_{\mathrm {total} }}{{A}_{\mathrm {total} }}}-{\frac {\sum _{i=1}^{N}{{A}_{i}}\ln {\frac {{E}_{i}}{{A}_{i}}}}{{A}_{\mathrm {total} }}}}$

En cas de ${\displaystyle {{E}'_{i}}=E_{i}/E_{\text{total}}}$ et ${\displaystyle {{A}'_{i}}=A_{i}/A_{\text{total}}}$:
${\displaystyle \color {Gray}T_{L}=0-{\frac {\sum _{i=1}^{N}{{A}'_{i}}\ln {\frac {{E}'_{i}}{{A}'_{i}}}}{1}}=\sum _{i=1}^{N}{{A}'_{i}}\ln {\frac {{A}'_{i}}{{E}'_{i}}}}$

L'opération[4] pour normaliser les indices de Theil est ${\displaystyle \displaystyle 1-e^{-T}}$

La moyenne de ces deux formules[5] est un indice symétrique :

${\displaystyle T_{s}={\frac {1}{2}}\sum _{i=1}^{N}\color {Blue}\ln {\frac {E_{i}}{A_{i}}}\left(\color {Black}{\frac {{E}_{i}}{E_{\text{total}}}}-{\frac {A_{i}}{A_{\text{total}}}}\color {Blue}\right)\color {Black}}$

La moyenne est très convenable par comparaison avec le plus simple des indices d'inégalité : l'indice de Hoover. La différence est indiquée par la couleur bleue.

${\displaystyle H={\frac {1}{2}}\sum _{i=1}^{N}\color {Blue}\left|\color {Black}{\frac {E_{i}}{E_{\text{total}}}}-{\frac {A_{i}}{A_{\text{total}}}}\color {Blue}\right|\color {Black}}$

Si pour les sous-groupes ${\displaystyle k}$ les sous-indices de Theil sont connus : ${\displaystyle T_{T}=\ln {\frac {{A}_{\mathrm {total} }}{{E}_{\mathrm {total} }}}-{\frac {\sum _{i=1}^{N}{{E}_{i}}\left(\ln {\frac {{A}_{i}}{{E}_{i}}}-T_{T_{i}}\right)}{{E}_{\mathrm {total} }}}}$

${\displaystyle T_{L}=\ln {\frac {{E}_{\mathrm {total} }}{{A}_{\mathrm {total} }}}-{\frac {\sum _{i=1}^{N}{{A}_{i}}\left(\ln {\frac {{E}_{i}}{{A}_{i}}}-T_{L_{i}}\right)}{{A}_{\mathrm {total} }}}}$

${\displaystyle T_{s}={\frac {1}{2}}\sum _{i=1}^{N}\ln {\frac {E_{i}}{A_{i}}}\left({\frac {{E}_{i}}{E_{\text{total}}}}-{\frac {A_{i}}{A_{\text{total}}}}\right)+{\frac {{E}_{i}}{E_{\text{total}}}}T_{T_{i}}+{\frac {{A}_{i}}{A_{\text{total}}}}T_{L_{i}}}$

Il est possible de calculer la fonction de bien-être (welfare function) proposée par Amartya Sen et James A. Foster (1996)[6] par cette formule :

${\displaystyle {W_{\text{Theil-L}}={\overline {revenu}}\cdot \mathrm {e} ^{-T_{L}}={\frac {E_{\mathrm {total} }}{A_{\mathrm {total} }}}{\text{ }}\mathrm {e} ^{-T_{L}}=\mathrm {e} ^{\frac {\sum _{i=1}^{N}{{A}_{i}}\left(\ln {\frac {{E}_{i}}{{A}_{i}}}-T_{L_{i}}\right)}{{A}_{\mathrm {total} }}}=\prod _{i=1}^{N}\left({\frac {{E}_{i}}{{A}_{i}}}\ \mathrm {e} ^{-T_{L_{i}}}\right)^{\frac {{A}_{i}}{{A}_{\mathrm {total} }}}}}$

Le revenu moyen d'une personne dans une société dont les revenus sont inégaux ne décrit pas le revenu ${\displaystyle E_{i}}$ de la majorité des citoyens. La fonction de bien-être peut remplacer la médiane. La valeur de la fonction de bien-être est toujours plus petite que le revenu moyen.

Si on prend un € du revenu total de cette société, cet € sera part d'un revenu ${\displaystyle E_{i}}$ plus grand que le revenu moyen :

${\displaystyle {W_{\text{Theil-T}}^{-1}={\overline {revenu}}\cdot \mathrm {e} ^{T_{T}}={\frac {E_{\mathrm {total} }}{A_{\mathrm {total} }}}{\text{ }}\mathrm {e} ^{T_{T}}=\mathrm {e} ^{\frac {\sum _{i=1}^{N}{{E}_{i}}\left(\ln {\frac {{E}_{i}}{{A}_{i}}}+T_{T_{i}}\right)}{{E}_{\mathrm {total} }}}=\prod _{i=1}^{N}\left({\frac {{E}_{i}}{{A}_{i}}}{\text{ }}\mathrm {e} ^{T_{T_{i}}}\right)^{\frac {{E}_{i}}{{E}_{\mathrm {total} }}}}}$

• Coefficient de Gini
• Serge-Christophe Kolm

• (en) Amiel, Y.: Thinking about inequality, Cambridge 1999.
• (en) Cowell, Frank A. (2002, 2003): Theil, Inequality and the Structure of Income Distribution, London School of Economics and Political Sciences (sur la classe des indices de Kolm)
• (en) Sen, Amartya: On Economic Inequality (Enlarged Edition with a substantial annexe “On Economic Inequality” after a Quarter Century with James Foster), Oxford 1997, (ISBN 0-19-828193-5)
• (en) Tsui, Kai-Yuen (1995): Multidimensional Generalizations of the Relative and Absolute Inequality Indices: The Atkinson-Kolm-Sen Approach. Journal of Economic Theory 67, 251-265.

• La répartition du revenu disponible (Répartition par tranche de revenu des ménages, Source : Insee. Année des données : 2004, enquête revenus fiscaux) et les mesures d'inégalité