Inégalité d'Hermite-Hadamard
En mathématiques, l'inégalité d'Hermite–Hadamard, nommé d'après Charles Hermite et Jacques Hadamard, parfois appelée inégalité de Hadamard, dit que si une fonction f:[a,b]→ℝ est convexe, alors son intégrale est bornée par :

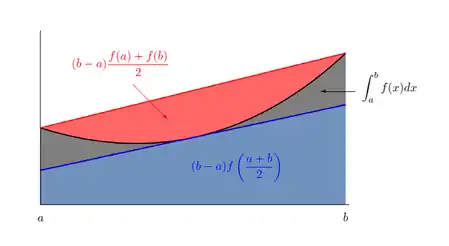
Illustration de l'inégalité d'Hermite-Hadamard.
Preuve
Si la fonction f est convexe sur un intervalle, elle y est continue, mais aussi dérivable à gauche et à droite en chaque point. On note f − et f + ces dérivées respectivement. Ainsi, pour chaque x0 ∈ [a,b], on peut construire une ligne
![{\displaystyle t(x)=f(x_{0})+c(x-x_{0}),\ c\in [f^{-}(x_{0}),f^{+}(x_{0})].}](https://img.franco.wiki/i/cf98150f8b57e5e1a8e51a93e4b63a6e4532f799.svg)
telle que
![{\displaystyle \forall x\in [a,b],t(x)\leqslant f(x),{\text{ et }}t(x)=f(x)\Leftrightarrow x=x_{0}.}](https://img.franco.wiki/i/59451b4269e7f119c4cb3da3325a04e001c8b429.svg)
On a, en particulier, pour x0=a+b/2 :
![{\displaystyle \forall x\in [a,b],f\left({\frac {a+b}{2}}\right)+c\left(x-{\frac {a+b}{2}}\right)\leqslant f(x),\ c\in \left[f^{-}\left({\frac {a+b}{2}}\right),f^{+}\left({\frac {a+b}{2}}\right)\right].}](https://img.franco.wiki/i/c4a8d32b73501ea0987a4bc1d1da13766c62095c.svg)
D'autre part, toujours par convexité de f, on a :
![{\displaystyle \forall x\in [a,b],f(x)\leqslant f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a).}](https://img.franco.wiki/i/6eeb6502cf15a8ee1d75a75e42c620050660bb19.svg)
Il suffit alors de calculer les intégrales des deux fonctions affines :
![{\displaystyle \int _{a}^{b}\left[f\left({\frac {a+b}{2}}\right)+c\left(x-{\frac {a+b}{2}}\right)\right]\,\mathrm {d} x=(b-a)f\left({\frac {a+b}{2}}\right),\ \int _{a}^{b}\left[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)\right]\,\mathrm {d} x=(b-a){\frac {f(a)+f(b)}{2}}.}](https://img.franco.wiki/i/4c5d97e91597ce76591b6da91f03637e4e666994.svg)
Généralisation par les intégrales itérées
On considère f:[a, b] → ℝ une fonction réelle intégrable. On peut définir la suite de fonctions suivante d'intégrales itérées de f, pour a ≤ s ≤ b.:

Alors si f est convexe, pour a < xi < b, i = 1, ..., n, distincts deux à deux (xi ≠ xj et i ≠ j), alors on a:

avec

L'inégalité change de sens si f est concave.
Le cas d'égalité est vérifié si et seulement si f est linéaire.
On a également : avec  pour
pour  alors
alors

Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Hermite–Hadamard inequality » (voir la liste des auteurs).
- Jacques Hadamard, "Étude sur les propriétés des fonctions entières et en particulier d'une fonction considérée par Riemann", Journal de mathématiques pures et appliquées, volume 58, 1893, pages 171–215.
- Zoltán Retkes, "An extension of the Hermite–Hadamard Inequality", Acta Sci. Math. (Szeged), 74 (2008), pages 95–106.
- Mihály Bessenyei, "The Hermite–Hadamard Inequality on Simplices", American Mathematical Monthly, volume 115, April 2008, pages 339–345.
- Flavia-Corina Mitroi, Eleutherius Symeonidis, "The converse of the Hermite-Hadamard inequality on simplices", Expo. Math. 30 (2012), pp. 389–396. DOI:10.1016/j.exmath.2012.08.011; (ISSN 0723-0869)
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.


![{\displaystyle t(x)=f(x_{0})+c(x-x_{0}),\ c\in [f^{-}(x_{0}),f^{+}(x_{0})].}](https://img.franco.wiki/i/cf98150f8b57e5e1a8e51a93e4b63a6e4532f799.svg)
![{\displaystyle \forall x\in [a,b],t(x)\leqslant f(x),{\text{ et }}t(x)=f(x)\Leftrightarrow x=x_{0}.}](https://img.franco.wiki/i/59451b4269e7f119c4cb3da3325a04e001c8b429.svg)
![{\displaystyle \forall x\in [a,b],f\left({\frac {a+b}{2}}\right)+c\left(x-{\frac {a+b}{2}}\right)\leqslant f(x),\ c\in \left[f^{-}\left({\frac {a+b}{2}}\right),f^{+}\left({\frac {a+b}{2}}\right)\right].}](https://img.franco.wiki/i/c4a8d32b73501ea0987a4bc1d1da13766c62095c.svg)
![{\displaystyle \forall x\in [a,b],f(x)\leqslant f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a).}](https://img.franco.wiki/i/6eeb6502cf15a8ee1d75a75e42c620050660bb19.svg)
![{\displaystyle \int _{a}^{b}\left[f\left({\frac {a+b}{2}}\right)+c\left(x-{\frac {a+b}{2}}\right)\right]\,\mathrm {d} x=(b-a)f\left({\frac {a+b}{2}}\right),\ \int _{a}^{b}\left[f(a)+{\frac {f(b)-f(a)}{b-a}}(x-a)\right]\,\mathrm {d} x=(b-a){\frac {f(a)+f(b)}{2}}.}](https://img.franco.wiki/i/4c5d97e91597ce76591b6da91f03637e4e666994.svg)





