Groupes de Curie

Les groupes de Curie sont notés en utilisant des symboles de Hermann-Maugin[2] - [3]: ${\displaystyle \infty }$ est un axe d'isotropie (axe de rotation d'angle quelconque), ${\displaystyle 2}$ est un axe binaire, ${\displaystyle m}$ est un miroir, ${\displaystyle /m}$ indique que le miroir est perpendiculaire à l'axe. On donne aussi, entre crochets, la notation originale de Curie. Chaque groupe est décrit par ses éléments de symétrie.

• ${\displaystyle \infty }$ [${\displaystyle (L_{\infty },l_{\infty })}$] : le seul élément de symétrie est l’axe d’isotropie ${\displaystyle \infty }$; le groupe est isomorphe à SO(2);

• ${\displaystyle \infty m}$ [${\displaystyle (L_{\infty },l_{\infty }),\infty P_{1}}$] : en plus de l’axe d’isotropie ${\displaystyle \infty }$, il y a un miroir (et donc une infinité de miroirs) contenant l’axe d’isotropie ${\displaystyle \infty }$; le groupe est isomorphe à O(2);

• ${\displaystyle \infty /m}$ [${\displaystyle (L_{\infty },l_{\infty })/P_{\infty },C}$)] : en plus de l’axe d’isotropie ${\displaystyle \infty }$, il y a un miroir perpendiculaire à l’axe ${\displaystyle \infty }$, et donc un centre de symétrie ${\displaystyle C}$ situé à l’intersection de l’axe ${\displaystyle \infty }$ et du plan de symétrie;

• ${\displaystyle \infty 2}$ [${\displaystyle 2L_{\infty }}$, ${\displaystyle \infty L_{2}}$] : en plus de l’axe d’isotrope ${\displaystyle \infty }$, il y a un axe binaire perpendiculaire (et donc une infinité d’axes binaires perpendiculaires) à l’axe ${\displaystyle \infty }$; il y a nécessairement un centre de symétrie ${\displaystyle C}$ à l’intersection commune des axes binaires;

• ${\displaystyle \infty /mm}$ [${\displaystyle 2L_{\infty }/P_{\infty },\infty L_{2}/\infty P_{2},C}$] : en plus de l’axe d’isotropie ${\displaystyle \infty }$, il y a un miroir perpendiculaire à l’axe ${\displaystyle \infty }$ et un miroir (et donc une infinité de miroirs) contenant l’axe d’isotropie ${\displaystyle \infty }$; il y a nécessairement un centre de symétrie ${\displaystyle C}$ à l’intersection commune des axes binaires;

• ${\displaystyle \infty \infty }$ [${\displaystyle \infty L_{\infty }}$] : toutes les droites passant par le point invariant sont des axes d’isotropie ${\displaystyle \infty }$; le groupe est isomorphe à SO(3);

• ${\displaystyle \infty \infty m}$ [${\displaystyle \infty L_{\infty },\infty P_{\infty },C}$] : en plus des axes d’isotropie ${\displaystyle \infty }$ du groupe ${\displaystyle \infty \infty }$, le groupe contient un miroir passant par le point invariant, donc tous les miroirs passant par le point invariant et aussi un centre de symétrie situé au point invariant; le groupe est isomorphe à O(3).

Le groupe de symétrie associé à un champ électrique est ${\displaystyle \infty m}$, tandis que celui associé à un champ magnétique est ${\displaystyle \infty /m}$.

L'ensemble des groupes de Curie est ordonné pour la relation d'inclusion et forme un treillis.

Diagramme d'inclusion des sept groupes de Curie.

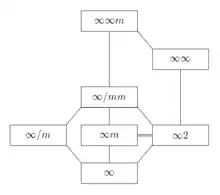
Le diagramme ci-contre montre les relations d'inclusion. L'inclusion est indiquée par un trait montant, vertical ou oblique. Le double trait horizontal entre ${\displaystyle \infty m}$ et ${\displaystyle \infty 2}$ indique qu'ils sont isomorphes.

Le groupe ${\displaystyle \infty \infty m}$ est l'unique élément maximal de l'ensemble (c'est-à-dire le maximum). Inversement, le groupe ${\displaystyle \infty }$ est l'unique élément minimal de l'ensemble (c'est-à-dire le minimum).

On calcule les indices de sous-groupes suivants:

Une rotation du groupe ${\displaystyle \infty }$ est indexée par un paramètre continu réel, alors qu'une rotation du groupe ${\displaystyle \infty \infty }$ est indexée par 3 paramètres réels (par exemple ses angles d'Euler). En résumé, on peut écrire formellement l'ordre des groupes de Curie ainsi[4] :

${\displaystyle |\infty |=\infty ,\;\;\;|\infty /m|=|\infty m|=|\infty 2|=2\infty ,\;\;\;|\infty /mm|=4\infty ,\;\;\;|\infty \infty |=\infty ^{3},\;\;\;|\infty \infty m|=2\infty ^{3}.}$

Rappelons que les groupes de Curie ont été introduits à propos de l'établissement du principe général de symétrie connu comme le principe de Curie. Selon ce principe, le groupe le groupe de symétrie ${\displaystyle {\mathsf {G_{cristal}}}}$ d'un cristal présentant une propriété physique ayant un groupe de symétrie ${\displaystyle {\mathsf {G_{prop}}}}$ est tel que ${\displaystyle {\mathsf {G_{cristal}\subseteq G_{prop}}}}$. Voyons deux exemples.

• La pyroélectricité. Sous l'effet de la chaleur, le cristal, sans modifier sa géométrie, va présenter une polarisation électrique spontanée. Les cristaux pyroélectriques ont donc pour groupe ponctuel de symétrie un sous-groupe du groupe de Curie ${\displaystyle \infty m}$ associé au champ électrique. Peuvent donc être pyroélectriques les seuls cristaux de groupe de symétrie parmi les 10 possibilités suivantes : ${\displaystyle 6mm}$, ${\displaystyle 6}$, ${\displaystyle 3m}$, ${\displaystyle 3}$, ${\displaystyle 4mm}$,${\displaystyle 4}$, ${\displaystyle mm2}$, ${\displaystyle m}$, ${\displaystyle 2}$, ${\displaystyle 1}$. Le vecteur polarisation se trouve alors le long de l'axe de symétrie (s'il existe) et est contenu dans le(s) plan(s) de symétrie (s'il(s) existe(nt)).
• la piézoélectricité. Le cas de la piézoélectricité n'est pas aussi simple que celui de la pyroélectricité car on doit raisonner sur la symétrie du cristal déformé. On montre qu'il existe 20 classes compatibles avec la piézoélectricité, dont les 10 classes pyroélectriques. Par exemple, le quartz a pour groupe d'espace ${\displaystyle P3_{1}21}$ de la classe ${\displaystyle 32}$. En comprimant le quartz le long d'un axe binaire, le cristal pourra présenter de la piézoélectricité.