Graphe de Robertson
Le graphe de Robertson est, en théorie des graphes, un graphe 4-régulier possédant 19 sommets et 38 arêtes.
| Graphe de Robertson | |
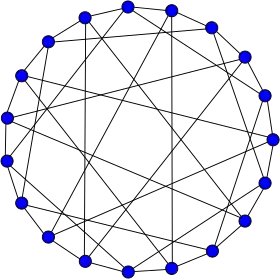 Représentation hamiltonienne du graphe de Robertson. | |
| Nombre de sommets | 19 |
|---|---|
| Nombre d'arêtes | 38 |
| Distribution des degrés | 4-régulier |
| Rayon | 3 |
| Diamètre | 3 |
| Maille | 5 |
| Automorphismes | 24 |
| Nombre chromatique | 3 |
| Indice chromatique | 5 |
| Propriétés | Cage Hamiltonien |
Propriétés
Propriétés générales
Le diamètre du graphe de Robertson, l'excentricité maximale de ses sommets, est 3, son rayon, l'excentricité minimale de ses sommets, est 3 et sa maille, la longueur de son plus court cycle, est 5. Il s'agit d'un graphe 4-sommet-connexe et d'un graphe 4-arête-connexe, c'est-à-dire qu'il est connexe et que pour le rendre déconnecté il faut le priver au minimum de 4 sommets ou de 4 arêtes.
Coloration
Le nombre chromatique du graphe de Robertson est 3. C'est-à-dire qu'il est possible de le colorer avec 3 couleurs de telle façon que deux sommets reliés par une arête soient toujours de couleurs différentes mais ce nombre est minimal. Il n'existe pas de 2-coloration valide du graphe.
L'indice chromatique du graphe de Robertson est 5. Il existe donc une 5-coloration des arêtes du graphe telle que deux arêtes incidentes à un même sommet soient toujours de couleurs différentes. Ce nombre est minimal.
Propriétés algébriques
Le groupe d'automorphismes du graphe de Robertson est un groupe d'ordre 24.
Le polynôme caractéristique de la matrice d'adjacence du graphe de Robertson est : .
