Géométrie des transformations
En mathématiques, la géométrie des transformations correspond à l'étude géométrique centrée sur les groupes de transformations géométriques et à leurs propriétés, indépendamment des figures, considérées invariantes. Elle s'oppose de façon claire à la géométrie euclidienne, qui se concentre sur la construction géométrique.
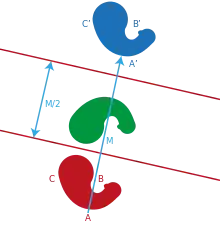
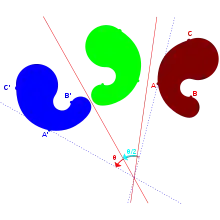
Par exemple, dans la géométrie des transformations, les propriétés d'un triangle isocèle sont déduites des symétries internes autour des droites géométriques particulières (hauteurs, bissectrices, médiatrices). Cette définition contraste avec la définition classique selon laquelle est isocèle tout triangle qui au moins deux angles égaux[1].
Au XIXe siècle, Felix Klein est le premier à utiliser la transformation comme fondement de la géométrie, et propose une refonte du système euclidien dans le programme d'Erlangen. Au XXe siècle, une généralisation a été proposée pour l'éducation. Andreï Kolmogorov inclut cette approche (avec la théorie des ensembles), comme partie intégrante de la réforme de la géométrie en Russie[2]. Les mathématiques modernes des années 1960 reprendront une telle conception.
Enseignement de la géométrie des transformations
L'étude de la symétrie dans la vie courante peut permettre une première approche de la géométrie des transformations. La transformation la plus simple est celle de la symétrie autour d'un axe ou d'une droite. La composition de deux symétries permet une rotation, quand les droites sont sécantes, ou une translation, quand les droites sont parallèles. Avec ces transformations, il est possible de déduire les isométries du plan euclidien (conservation des angles et des longueurs).
De plus, en considérant les symétries S1 autour d'un axe vertical et S2 autour d'un axe incliné à 45° par rapport à l'horizontale (allant d'en bas à gauche à en haut à droite), l'application de S1 puis de S2 correspond à une rotation d'un quart de tour dans le sens horaire, tandis que l'application de S2 puis de S1 correspond à une rotation d'un quart de tour dans le sens anti-horaire. Un tel exemple montre que la géométrie des transformations contient des processus non commutatifs.
La géométrie des transformations présente une vision alternative contrastant avec la géométrie classique, et permettant d'ouvrir la voie pour la géométrie analytique ou l'algèbre linéaire (dans laquelle le concept de symétrie est étendu). En effet, on peut également exprimer la géométrie des transformations grâce à des nombres complexes, hypercomplexes, ou grâce à des matrices.
Dans son essai de restructuration des cours de géométrie en Russie, Kolmogorov suggérait de présenter la discipline en rapport avec la théorie des ensembles, faisant apparaître dans les écoles le terme de congruence géométrique ou d'égalité entre les figures : deux figures sont égales si et seulement si l'une peut être transformée en l'autre par isométries successives (translations, rotations, homothéties), et réciproquement[2].
Références
- Georges Glaeser, « La crise de l’éducation géométrique », dans Robert Morris, Études sur l’enseignement des mathématiques, vol. 5 : L’enseignement de la géométrie, Paris, UNESCO, coll. « L’enseignement des sciences fondamentales », (ISBN 92-3-202373-3, présentation en ligne, lire en ligne [PDF]), p. 113–128
- (en) Alexander Karp et Bruce R. Vogeli, Russian Mathematics Education: Programs and Practices, 2011, p. 100-102 sur Google Livres.
Voir aussi
Bibliographie
- (en) Heinrich Guggenheimer (en), Plane Geometry and Its Groups, Holden-Day, 1967
- (en) Roger Howe (en) et William Barker, Continuous Symmetry: From Euclid to Klein, AMS, 2007 (ISBN 978-0-8218-3900-3).
- (en) Robin Hartshorne, « Review of Continuous Symmetry », American Mathematical Monthly, vol. 118, 2011, p. 565-568
- (en) Max Jeger, Transformation Geometry (trad. de l'allemand), 1966
- (ru) A. N. Kolmogorov. Геометрические преобразования в школьном курсе геометрии, Математика в школе, 1965, Nº 2, p. 24-29 (Geometric transformations in a school geometry course)
- (en) Roger Lyndon, Groups and Geometry, coll. « London Mathematical Society Lecture Note Series » (no 101), Cambridge University Press, 1985 (ISBN 0-521-31694-4)
- (en) George E. Martin, Transformation Geometry: An Introduction to Symmetry, Springer Verlag, 1982
- (en) P. S. Modenov et A. S. Parkhomenko, Geometric Transformations, trad. Michael B.P. Slater, Academic Press, 1965
- (en) Alton T. Olson, High School Plane Geometry Through Transformations: An Exploratory Study, vol. I et II, University of Wisconsin-Madison,
- (en) Nathalie Sinclair, The History of the Geometry Curriculum in the United States, 2008, p. 63-66 sur Google Livres
- (en) Zalman P. Usiskin et Arthur F. Coxford, « A Transformation Approach to Tenth Grade Geometry », The Mathematics Teacher, vol. 65, no 1, 1972, p. 21-30, JSTOR:27958671
- (en) Zalman P. Usiskin, « The Effects of Teaching Euclidean Geometry via Transformations on Student Achievement and Attitudes in Tenth-Grade Geometry », Journal for Research in Mathematics Education, vol. 3, no 4, 1972, p. 249-259, JSTOR:748492
- (en) Isaak Yaglom (en), Geometric Transformations (trad. du russe), Random House, 1962
Lien externe
(en) Transformations teaching notes from Gatsby Charitable Foundation