Génération d'harmonique

La génération d'harmonique (GH, HG (en) aussi appelée génération d'harmonique d'ordre n) est un processus d'optique non linéaire dans lequel n photons avec la même fréquence interagissant avec un milieu non linéaire, se « combinent » générant un nouveau photon avec n fois l'énergie des photons initiaux (de manière équivalente, n fois la fréquence et de longueur d'onde divisée par n).

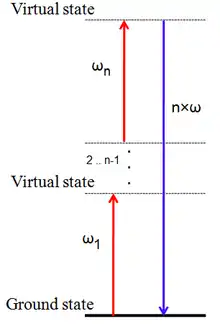
Génération de la n-ième harmonique. Ground state = niveau fondamental, virtual state = niveau virtuel.

Processus général

Dans un milieu ayant une susceptibilité non linéaire suffisamment grande, la génération d'harmonique est possible. Notez que pour les ordres pairs (n = 2, 4, ...), le milieu ne doit pas avoir de centre de symétrie (être non-centrosymétrique)[1].

Du fait que le processus nécessite que de nombreux photons soient présents en même temps et au même endroit, la génération d'harmonique a une faible probabilité de se produire, et cette probabilité diminue avec l'ordre n (car besoin de plus de photons). Pour générer efficacement, la symétrie du milieu doit permettre d'amplifier le signal (par accord de phase par exemple), et la source lumineuse doit être intense et bien contrôlée spatialement (grâce à un laser collimaté) et temporellement (plus de signal généré si le laser a de courtes impulsions)[2].

Génération de somme de fréquence (SFG)

Cas spécial où le nombre de photons en interaction est n = 2, mais avec deux photons de pulsations différentes $\omega _{1}$ et $\omega _{2}$ .

Génération de seconde harmonique (SHG)

Cas spécial où le nombre de photons en interaction est n = 2, avec deux photons de même pulsation $\omega$ . C'est aussi un cas particulier de SFG où les 2 photons ont la même fréquence.

Génération de troisième harmonique (THG)

Un cas particulier où le nombre de photons en interaction est n = 3, si tous les photons ont la même pulsation $\omega$ . S'ils ont des fréquences différentes, c'est un processus de mélange à quatre ondes, plus général. Ce processus implique la susceptibilité non linéaire du 3^e ordre $\chi ^{(3)}$ [3].

Contrairement à la SHG, c'est un processus volumétrique [4] et a été démontrée dans des liquides [5]. Cependant, elle est exaltée aux interfaces [6].

Materiaux utilisés pour la THG

Des cristaux non linéaires comme le BBO (β-BaB₂O₄) ou le LBO peuvent convertir de la THG. Sinon, de la THG peut être générée à partir de membranes en microscopie [7].

Génération de 4^e harmonique (FHG or 4HG)

Cas spécial où le nombre de photons en interaction est n = 4. Prouvée expérimentalement vers les années 2000 [8], des lasers puissants permettent désormais de générer de la FHG efficacement. Ce processus implique la susceptibilité non linéaire du 4^e ordre $\chi ^{(4)}$ .

Materiaux utilisés pour la FHG

Certains BBO (β-BaB₂O₄) sont utilisés pour la FHG [9].