Formule quadratique

En algèbre classique, la formule quadratique est la solution de l'équation du second degré. Il y a d'autres façons pour résoudre l'équation du second degré au lieu d'utiliser la formule quadratique, comme la factorisation, la méthode de complétion du carré ou le tracé du graphe. Mais utiliser la formule quadratique est souvent la façon la plus pratique.

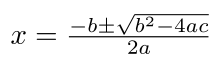
La formule quadratique sous forme contractée.

L'équation du second degré générale est :

ax^{2}+bx+c=0.

Ici, $x$ représente une valeur inconnue alors que $a$ , $b$ et $c$ sont constantes, avec $a$ non nul. En insérant la formule quadratique dans l'équation du second degré, on peut vérifier que la formule quadratique satisfait l'équation du second degré. Les deux solutions données par la formule quadratique sont les racines de l'équation.

Démonstration

Quand les élèves apprennent la méthode de complétion du carré, ils peuvent en déduire la formule quadratique[1] - [2]. Pour cette raison, la démonstration de la formule quadratique leur est parfois laissée en exercice, pour leur permettre de la redécouvrir[3] - [4]. Si (par exemple) $a,b,c$ sont des nombres complexes (avec $a\neq 0$ ), les solutions de $ax^{2}+bx+c=0$ sont[5] :

x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\quad {\text{et}}\quad x={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}

où ${\sqrt {b^{2}-4ac}}$ désigne une racine carrée de $b^{2}-4ac$ . Une démonstration figure dans l'article sur l'équation du second degré.

Références

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Quadratic formula » (voir la liste des auteurs).

(en) Barnett Rich et Philip Schmidt, Schaum's Outline of Theory and Problems of Elementary Algebra, McGraw-Hill, 2004, 400 p. (ISBN 0-07-141083-X, lire en ligne), « 13 §4.4 », p. 291.
(en) Xuhui Li,An Investigation of Secondary School Algebra Teachers' Mathematical Knowledge for Teaching Algebraic Equation Solving, ProQuest, 2007, p. 56 sur Google Livres : « The quadratic formula is the most general method for solving quadratic equations and is derived from another general method: completing the square. »
(en) Gary Rockswold, College Algebra and Trigonometry and Precalculus, Addison Wesley, 2002, p. 178.
(en) Edwin F. Beckenbach, Irving Drooyan et Michael D. Grady, Modern College Algebra and Trigonometry, Wadsworth Pub., 1986, p. 81.
(en) Mary Jane Sterling, Algebra I For Dummies, Wiley, 2016, 384 p. (ISBN 978-1-119-29357-6, lire en ligne), p. 223.

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.