Complétion du carré
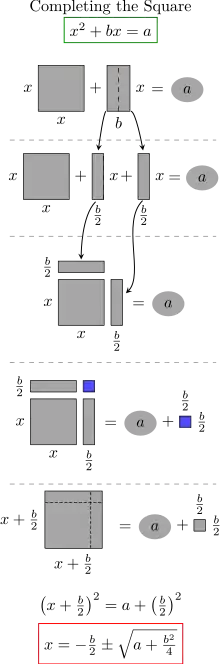
Méthode
L'idée générale de cette technique consiste, partant d'une équation de la forme A+B=C, à la mettre sous la forme A+B+D=C+D, où D est choisi pour que A+B+D soit le développement d'une identité remarquable telle que  (une variante de ce procédé consiste à « ajouter 0 », c'est-à-dire à écrire A+B sous la forme A+B+D-D). Ainsi, lorsqu'on a une équation de la forme
(une variante de ce procédé consiste à « ajouter 0 », c'est-à-dire à écrire A+B sous la forme A+B+D-D). Ainsi, lorsqu'on a une équation de la forme  on ajoute
on ajoute  de chaque côté de l'équation pour faire apparaître
de chaque côté de l'équation pour faire apparaître  , ce qui donne
, ce qui donne
 ,
,
d'où ![{\displaystyle \left[x+\left({\frac {b}{2}}\right)\right]^{2}=\left({\frac {b}{2}}\right)^{2}-c}](https://img.franco.wiki/i/2a6cca24661ebd882105a197136671e5ab2af2df.svg)
et donc  (en supposant que le radicande soit positif).
(en supposant que le radicande soit positif).
- Exemple
Soit  l'équation à résoudre. On ajoute
l'équation à résoudre. On ajoute  de chaque côté.
de chaque côté.
On obtient  ,
,
qui se simplifie en  ,
,
puis en 
et enfin  .
.
D'où les solutions de l'équation,  et
et  .
.
Généralisation
On peut appliquer cette méthode à une équation de la forme  , où
, où 

 car
car 
En appliquant à cette équation la méthode ci-dessus, on obtient la forme canonique
 ;
;
on retrouve alors la formule de Viète (en supposant le radicande positif) :

ou sous une forme plus habituelle, avec le discriminant du polynôme :
 ;
;  .
.
Si le discriminant est positif, on obtient la factorisation canonique :

Autres applications
La même idée peut s’appliquer à d’autres expressions algébriques ; elle permet par exemple de transformer une équation cartésienne comme  en
en  ou encore
ou encore  ; on reconnait alors l'équation d'un cercle de centre (-1, 2) et de rayon 3.
; on reconnait alors l'équation d'un cercle de centre (-1, 2) et de rayon 3.
On peut également obtenir de même l’identité de Sophie Germain :

La complétion du carré est également utile pour le calcul de certaines intégrales. Ainsi, pour une intégrale de la forme
 , réécrite
, réécrite  ,
,
on peut revenir, en posant  , à des formes dont on peut calculer les primitives à partir des fonctions usuelles :
, à des formes dont on peut calculer les primitives à partir des fonctions usuelles :
 .
.
Cet article est issu de
wikipedia. Text licence:
CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.
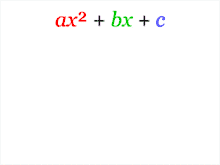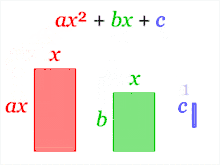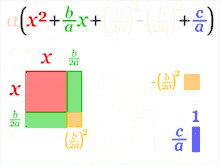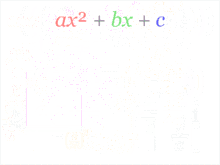








![{\displaystyle \left[x+\left({\frac {b}{2}}\right)\right]^{2}=\left({\frac {b}{2}}\right)^{2}-c}](https://img.franco.wiki/i/2a6cca24661ebd882105a197136671e5ab2af2df.svg)























