Fontaine de Galilée
La fontaine de Galilée ou boule de Galilée est une structure installée dans le parc du Près-La-Rose à Montbéliard[1]. Elle est constituée d'une sphère de granit de près d'un mètre de diamètre posé dans un socle. Malgré sa masse supérieure à une tonne, un dispositif hydraulique simple permet même à un enfant de la mettre en rotation.

| Type | |
|---|---|
| Construction |
1991 |
| Pays | |
|---|---|
| Région | |
| Département | |
| Commune | |
| Adresse |
Parc du Près-La-Rose |
| Gare | |
|---|---|
| Autobus |
| Coordonnées |
47° 30′ 20″ N, 6° 47′ 56″ E |
|---|
 |
 |
Elle a été construite dans les Vosges et posée le mardi dans le parc du Près-La-Rose à Montbéliard. Conçue dans un granit de Suède pur[2] d'une masse avoisinant 1 500 kg[1], elle a nécessité l'utilisation d'une grue de 60 tonnes pour sa mise en activité. Le principe est assez simple dans son ensemble, elle repose sur le principe d'un mouvement rectiligne, uniforme et constant dû à l'élimination des forces de frottement. Bien qu'assez compréhensible, cette installation est tout de même assez impressionnante par sa conception et par les lois physiques sur lesquelles elle repose.
Place au sein du parc
Située au milieu de l'allée centrale du parc[3], elle accueille et met les visiteurs en contact avec les sciences et la physique de façon ludique. En effet les forces de frottement étant quasi annihilées par le système hydraulique de la structure, il est ainsi possible de la faire tourner sur son support grâce à une faible force (celle d'un enfant) rendu possible par l'inertie de la Boule qui est toujours présente.
Premier Principe de Fonctionnement
La boule de granit est posée sur un socle de 20 cm de profondeur. En théorie il serait impossible de la faire tourner car sa masse et les forces de frottements nécessiteraient une force équivalente à près d'une tonne pour la bouger. Néanmoins le mécanisme hydraulique de l'installation permet d'éliminer les forces pressantes grâce à une pompe délivrant un débit de 0,5 litre par seconde et permet l'équilibre de la boule sur cette mince couche d'eau d'environ 0,1 millimètre. De ce fait la pression (500 g/cm2) exercée par la pompe compense les forces de frottement. Seule l'inertie de la boule est à prendre en compte pour sa mise en rotation[1].
Si l'eau était simplement introduite comme film statique le poids de la boule la chasserait immédiatement d'où la nécessité de maintenir une pression constante.
La boule reste en équilibre grâce aux forces de pression du film d'eau. Le vecteur bleu représente la réaction du support (filet d'eau).
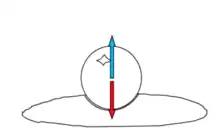
Pression d'équilibre statique
La pression différentielle Δp permet le bon maintien de la boule sur le film[1]. Cette pression est calculée selon le périmètre du support. La valeur de l'angle étant établie nous pouvons mesurer la hauteur restante de la boule et mettre en commun les deux résultats.
On connait donc la partie de la boule sur laquelle vont s'exercer les forces de pression.
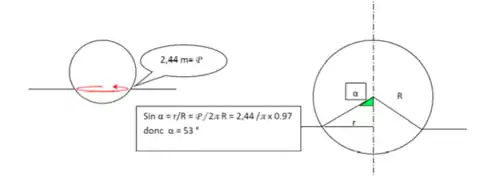 Pression d'équilibre statique
Pression d'équilibre statique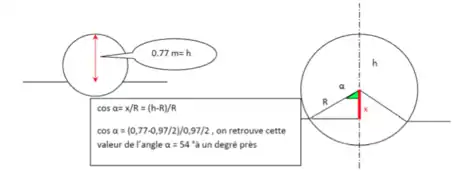 Pression d'équilibre statique 2
Pression d'équilibre statique 2
Calcul de Pression
La pression différentielle Δp= p(eau)-p(atmosphère) peut être aisément calculable[1].
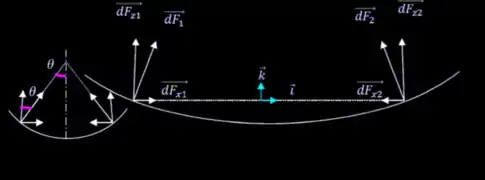
Pour cela il faut isoler une petite partie de la surface en contact avec le film d'eau : on obtient :
Seules les forces sur l'axe z sont à prendre en compte car les forces sur l'axe des x s'annulent par effet de symétrie. On a donc : Mettons maintenant en évidence une petite aire surfacique dS en coordonnée sphérique soumis à cette pression.
Donc :
 Calcul de Pression 2
Calcul de Pression 2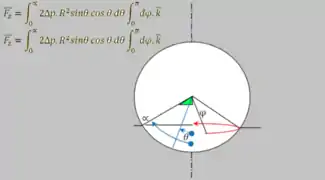 Calcul de Pression 3
Calcul de Pression 3
Or :
On a également :
Finalement :
On obtient donc l’équilibre statique de la boule soumise entre son poids et la pression exercée par l'eau écrit ainsi :
On en déduit la valeur de surpression nécessaire au fonctionnement du dispositif :
"Ce calcul ne donne que la valeur minimale pour que la boule soit en équilibre, on a enfin :"
Cette pression permet de maintenir la boule à 0,1 mm du sol.
Historique

De nombreuses théories en vigueur fondée ou non tentant d'expliquer le mouvement de rotation de cette boule ont été interprétées par diverses philosophes et scientifiques :
Antiquité : selon Aristote (-384 ; -322) le mouvement de la boule s’arrête si l’action du ′′moteur ′′ cesse, c'est-à-dire si celui qui l’a fait tourner arrête de provoquer ce mouvement. Ce mouvement ne peut se préserver de lui-même.
XIVe siècle : selon Buridan, le « moteur » du mouvement est celui qui fait tourner la sphère.
XVIIe siècle : selon Galilée, le mouvement de la Boule est possible sans cause.
1629 : Descartes énonce correctement en premier le fameux principe d’inertie. « Si je pousse cette sphère sur une surface horizontale et si je la lâche, elle poursuit sa route avec une vitesse constante sauf si un choc vient déranger ce mouvement ».
1687 : selon Newton, faire glisser sans frottement sur une surface horizontale parfaitement polie une sphère de granite c’est possible parce que l’on aura « supprimé le poids de cette sphère » et il ne faudra plus lutter que contre sa masse.
1750 : grâce à Euler puis Lagrange, on peut ainsi dire que le dispositif ici présent compense le poids et qu’il ne reste plus qu’à créer une action faisant tourner la boule sur elle-même malgré son moment d’inertie.
Autre dispositif
On distingue un autre dispositif dans le même registre : un mégalithe sur un axe vertical qui lui aussi peut être mis en mouvement par un enfant. Un roulement à billes qui minimise les frottements au niveau de l’axe de rotation permet cette prouesse.
D’un point de vue explicatif la situation est quasiment identique à celle vue pour la boule de Galilée sauf qu’ici l’axe de rotation n’est pas décidé par celui qui veut pousser la boule mais par son concepteur dès l’origine… Il est fixe par rapport à la Terre, vertical et passe par le centre de gravité du monolithe.
Un autre modèle, plus simple mathématiquement, existe également : celui de la roue de granite. En effet, l'axe de rotation étant fixé, il est alors très simple d'en étudier les caractéristiques physiques, telles que le temps de relaxation, dont un rapide calcul (quoiqu'assez dense) nous donne une tendance d'exponentielle décroissante avec le temps[4].
Références
- Fontaine de Galilée ac-Besancon
- Parc de Montbéliard : Fontaine de Galilée
- PARC SCIENTIFIQUE DU PRÈS-LA-ROSE
- (en) Jacco H. Snoeijer and Ko van der Weele, « Physics of the granite sphere fountain », American Journal of Physics,
Galerie Photos
 Fontaine de Galilée 1
Fontaine de Galilée 1 Fontaine de galilee 2
Fontaine de galilee 2 Fontaine de Galilée 3
Fontaine de Galilée 3 Fontaine de Galilée 4
Fontaine de Galilée 4 Fontaine de Galilée 5
Fontaine de Galilée 5










