Fonction de partition de Kostant
En théorie des représentations, un domaine des mathématiques, la fonction de partition de Kostant, introduite par Bertram Kostant[1] - [2], d'un système de racines , est le nombre de façons dont on peut représenter un vecteur (poids) comme combinaison linéaire à coefficients naturels des racines positives . Kostant l'a utilisée pour réécrire la formule des caractères de Weyl comme une formule, appelée formule de multiplicité de Kostant, donnant la multiplicité d'un poids d'une représentation irréductible d'une algèbre de Lie semi-simple. On dispose d'une autre formule, plus efficace en termes de calcul dans certains cas, appelée formule de Freudenthal.
La fonction de partition de Kostant peut également être définie pour les algèbres de Kac-Moody et a des propriétés similaires.
Un exemple
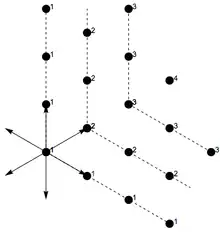
Considérons le système de racines de type A2, dont on note , et les racines positives. Si un élément peut être exprimé comme une combinaison linéaire à coefficients entiers naturels de , , et , alors, vu que , il peut également être exprimé comme une combinaison linéaire entière positive de et :
avec et étant des entiers naturels. Cette expression donne une façon d'écrire comme une combinaison entière à coefficients entiers naturels de racines positives ; d'autres expressions peuvent être obtenues en remplaçant par un certain nombre de fois. On peut faire cette substitution fois, où . Ainsi, en notant la fonction de partition de Kostant, on obtient la formule
- .
Ce résultat est représenté graphiquement sur l'image ci-contre. Bien sûr, si un élément n'est pas de la forme , alors .
Lien avec la formule des caractères de Weyl
Inversion du dénominateur de Weyl
Pour chaque racine et chaque , on peut appliquer formellement la formule de la somme d'une série géométrique pour obtenir
où l'on ne se soucie pas de la convergence, c'est-à-dire que l'égalité est comprise au niveau des séries de puissances formelles. En utilisant la formule du dénominateur de Weyl
on obtient une expression formelle de l'inverse du dénominateur de Weyl[3] :
Ici, la première égalité consiste à prendre le produit sur toutes les racines positives de la formule de la série géométrique et la seconde égalité consiste à compter toutes les façons dont une exponentielle donnée peut apparaître dans le produit.
Réécriture de la formule des caractères
Cet argument montre que l'on peut réécrire la formule des caractères de Weyl pour la représentation irréductible de plus haut poids
et la transformer de quotient en produit :
La formule de multiplicité
En utilisant la réécriture précédente de la formule des caractères, il est relativement facile d'écrire le caractère comme une somme d'exponentielles. Les coefficients de ces exponentielles sont les multiplicités des poids correspondants. On obtient ainsi une formule pour la multiplicité d'un poids donné dans la représentation irréductible de plus haut poids [4] :
- .
Ce résultat est la formule de multiplicité de Kostant.
Le terme dominant dans cette formule est le terme correspondant à ; la contribution de ce terme est , qui est juste la multiplicité de dans le module de Verma de plus haut poids . Si est suffisamment loin des murs à l'intérieur de la chambre fondamentale de Weyl et si est suffisamment proche de , il peut arriver que tous les autres termes de la formule soient nuls. Plus précisément, à moins que ne soit plus grand que , la valeur de la fonction de partition de Kostant en est nulle. Ainsi, bien que la somme porte initialement sur tout le groupe de Weyl, dans la plupart des cas, le nombre de termes non nuls est inférieur à l'ordre du groupe de Weyl.
Notes et références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Kostant partition function » (voir la liste des auteurs).
- Kostant 1958.
- Kostant 1959.
- Hall 2015, Proposition 10.27.
- Hall 2015, Theorem 10.29.
- Brian C. Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, vol. 222, Springer, coll. « Graduate Texts in Mathematics », (ISBN 978-3319134666)
- James E. Humphreys, Introduction to Lie Algebras and Representation Theory, Birkhäuser, 1972a (ISBN 978-0-387-90053-7, lire en ligne
 )
) - Bertram Kostant, « A formula for the multiplicity of a weight », Proceedings of the National Academy of Sciences, National Academy of Sciences, vol. 44, no 6, , p. 588-589 (ISSN 0027-8424, PMID 16590246, PMCID 528626, DOI 10.1073/pnas.44.6.588
 , JSTOR 89667, Bibcode 1958PNAS...44..588K, MR 0099387)
, JSTOR 89667, Bibcode 1958PNAS...44..588K, MR 0099387) - Bertram Kostant, « A formula for the multiplicity of a weight », Transactions of the American Mathematical Society, American Mathematical Society, vol. 93, no 1, , p. 53-73 (ISSN 0002-9947, DOI 10.2307/1993422
 , JSTOR 1993422, MR 0109192)
, JSTOR 1993422, MR 0109192)






























