Fonction Carotid–Kundalini

La fonction Carotid-Kundalini $CK_{n}$ est définie pour tout entier relatif n et pour tout réel x compris entre -1 et 1 par[1] :

CK_{n}(x)=cos(nx\arccos(x))

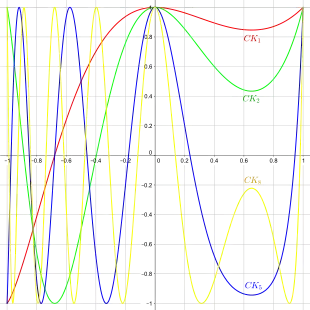
Fonction Carotid-Kundalini pour :
㇐ n=1
㇐ n=2
㇐ n=5
㇐ n=8

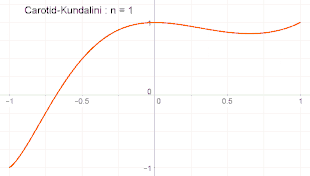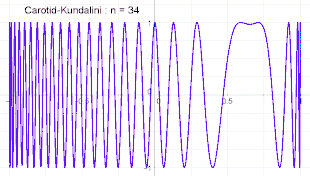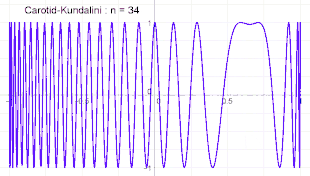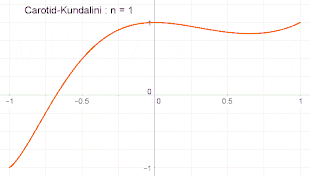
Graphe de la fonction Carotid-Jundalini pour différentes valeurs de n.

La fonction cosinus étant paire on a $CK_{n}=CK_{-n}$

Fractale

Fractale Carotid-Kundalini.

La fonction Carotid-Kundalini est directement associée à la fractale Carotid-Kundalini, qui s'obtient en empilant le graphe de la fonction pour différentes valeurs de n[2].

Elle est composée de trois régions nommées par Clifford Pickover[3] :

La "vallée fractale" (Fractal Valley), pour x compris entre -1 et 0. C'est dans cette région que l’empilement des graphes des fonctions semble adopter un comportement fractal ;
La "montagne gaussienne" (Gaussian Montain), la zone centrale, pour x ≈ 0 ;
Les "terres de l'oscillation" (Oscillation Land), pour x compris entre 0 et 1.

Notes et références

(en) « Carotid-Kundalini Function », sur mathworld.wolfram.com
(en) « Carotid-Kundalini Fractal », sur mathworld.wolfram.com
(en) « Carotid-Kundalini Functions », sur sprott.physics.wisc.edu

Liens externes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.