Figures de Brocard
Les figures de Brocard tirent leur nom du mathématicien français Henri Brocard (1845 -1922).
En réalité, elles ont été trouvées par Jacobi (1804 -1851) et, dès 1816, par Crelle.
Elles permettent de déterminer graphiquement les points de Brocard.
Points de Brocard

Les points de Brocard du triangle ABC sont les deux points intérieurs P et P' tels que, pour le premier, les angles orientés positivement soient égaux, et négativement pour le second.
Angle de Brocard
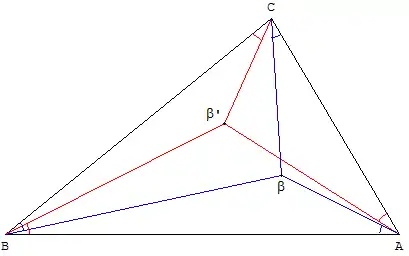
Les segments joignant les points de Brocard aux sommets du triangle constituent des isogonales particulières du triangle ABC.
Leur propriété remarquable est de définir toujours le même angle ω, dit angle de Brocard du triangle.
Formules pour l'angle de Brocard
Si est l'aire du triangle ABC, on peut calculer l'angle de Brocard à l'aide d'une des formules suivantes :
Pour cet angle on a :
Triangle de Brocard
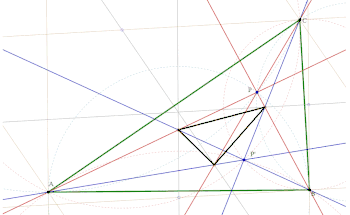
En géométrie, le triangle de Brocard est un triangle associé à un triangle donné, et construit à partir des points de Brocard de ce dernier.
Définition
Les premières (resp. secondes) droites de Brocard d'un triangle étant les droites joignant un sommet au premier (resp. second) point de Brocard, le triangle de Brocard d'un triangle ABC est formé par
- le point d'intersection de la première droite de Brocard issue de A avec la deuxième droite de Brocard issue de B (en bleu ci-contre)
- le point d'intersection de la première droite de Brocard issue de B avec la deuxième droite de Brocard issue de C
- le point d'intersection de la première droite de Brocard issue de C avec la deuxième droite de Brocard issue de A
Propriétés
Le triangle de Brocard a pour cercle circonscrit le cercle de Brocard.
Voir aussi
Articles connexes
Liens externes
- (en) Eric W. Weisstein, « First Brocard Triangle », sur MathWorld
- (en) Eric W. Weisstein, « Second Brocard Triangle », sur MathWorld
- Bernard Gibert, Brocard triangle and relative cubics.
- Triangles co-Brocardaux






