Cercle de Brocard
En géométrie, le cercle de Brocard d'un triangle est le cercle passant par les points de Brocard, le centre du cercle circonscrit et le point de Lemoine du triangle[1]. Il a pour diamètre le segment ayant pour extrémités le centre du cercle circonscrit et le point de Lemoine — la droite reliant ces deux points est appelée « axe de Brocard ». Le centre de ce cercle porte le nombre de Kimberling X182.
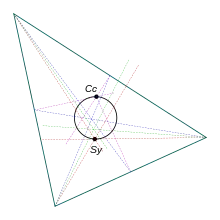
Dans le triangle est inscrit un cercle de Brocard.
Le cercle tire son nom du mathématicien Henri Brocard[2].
Le rayon du cercle de Brocard a pour valeur (avec a, b et c les longueurs des côtés et R le rayon du cercle circonscrit):
Notes et références
Articles connexes
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.
