Fiabilité structurelle

La fiabilité structurelle est la science de l'application des théories de l'ingénierie de la fiabilité aux bâtiments et autres structures[1] - [2]. Il est également utilisé comme méthode pour décrire la sécurité structurelle. La fiabilité d'une structure est définie comme la probabilité de complément de défaillance (Fiabilité = 1 - Probabilité de défaillance). La défaillance se produit lorsque la charge totale appliquée est supérieure à la résistance totale de la structure. La fiabilité structurelle est devenue connue comme une philosophie de conception au XXI^e siècle, et elle pourrait remplacer les méthodes déterministes traditionnelles de conception[3] et de maintenance[1].

La défaillance se produit lorsque les charges (S) sont plus grandes que la résistance (R)

Théorie

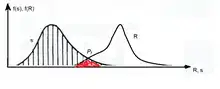
Les charges et les résistances sont modélisées comme des variables probabilistes. En utilisant cette approche, la probabilité de défaillance d'une structure est calculée. Lorsque les charges et les résistances sont explicites et ont leur propre fonction indépendante, la probabilité de défaillance peut être formulée comme suit[1] - [4].

$P_{f}=\int _{0}^{\infty }F_{R}(s)f_{s}(s)\,ds\qquad \mathrm {(1)}$

où Pf est la probabilité de défaillance, $F_{R}(s)$ est la fonction de distribution cumulative de la résistance (R) et $f_{s}(s)$ est la densité de probabilité de la charge (S).

Mais en réalité, la distribution des charges et des résistances n'est généralement pas indépendante, et la probabilité de défaillance est définie par la formule suivante.

$P_{f}=\int \int \int _{G(X)}f_{X}(X)\,dX\qquad \mathrm {(2)}$

où 𝑋 est le vecteur des variables de base, et G (X) qui est appelée est la fonction d'état limite pourrait être une ligne, une surface ou un volume dont l'intégrale est prise sur sa surface.

Approches de solution

Solutions exactes

Lorsque la charge et la résistance sont explicitement exprimées (comme l'équation (1) ci-dessus) et que leurs distributions sont normales, l'intégrale de l'équation (1) a une solution de forme fermée comme suit[1].

$p_{f}=1-\Phi (\beta ),$ $\beta ={\frac {\mu _{R}-\mu _{S}}{\sqrt {\sigma _{R}^{2}+\sigma _{S}^{2}}}}\qquad \mathrm {(3)}$

Méthode de Monte-Carlo

Souvent, la charge et la résistance ne sont pas normalement distribuées. Par conséquent, la résolution analytique des intégrales des équations (1) et (2) est impossible. L'utilisation de la simulation de Monte Carlo est une approche qui pourrait être utilisée dans de tels cas[1] - [4].

Références

(en) Sayed Madeh Piryonesi et Mehdi Tavakolan, « A mathematical programming model for solving cost-safety optimization (CSO) problems in the maintenance of structures », KSCE Journal of Civil Engineering, vol. 21, n^o 6,‎ septembre 2017, p. 2226–2234 (ISSN 1226-7988 et 1976-3808, DOI 10.1007/s12205-017-0531-z, lire en ligne, consulté le 8 octobre 2020)
Melchers, R. E. (2002), “Structural Reliability Analysis and Prediction,” 2nd Ed., John Wiley, Chichester, UK.
Choi, S. K., Grandhi, R., & Canfield, R. A. (2006). Reliability-based structural design. Springer Science & Business Media.
« Massih, D. Y. A., & Soubra, A. H. (2010). Analyse et dimensionnement fiabilistes des fondations superficielles filantes avec ou sans prise en compte des efforts sismiques pseudo-statiques. Revue Française de Géotechnique, (130), 25-39. »

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.