Loi de probabilité à plusieurs variables

La probabilité pour que la variable aléatoire ${\displaystyle X\,}$ prenne une valeur numérique inférieure à ${\displaystyle x\,}$ alors que ${\displaystyle Y\,}$ prend une valeur inférieure à ${\displaystyle y\,}$ définit la fonction de répartition [1]^{:p. 89}:

${\displaystyle F_{XY}(x,y)=\mathbb {P} (X\leq x,Y\leq y)}$

Celle-ci est non décroissante en ${\displaystyle x\,}$ et en ${\displaystyle y\,}$ entre la valeur 0 lorsque les deux variables tendent vers ${\displaystyle -\infty \,}$ et la valeur 1 lorsqu'elles tendent toutes deux vers ${\displaystyle +\infty \,}$.

La densité de probabilité jointe ou loi jointe s'obtient par une double dérivation :

${\displaystyle f_{XY}(x,y)={\frac {\partial ^{2}}{\partial x\,\partial y}}F_{XY}(x,y)}$

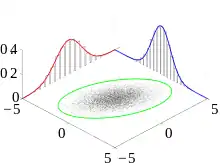
Une intégration par rapport à ${\displaystyle y\,}$ (resp. ${\displaystyle x\,}$) donne la densité de probabilité marginale ou loi marginale de ${\displaystyle X\,}$(resp. ${\displaystyle Y\,}$) :

${\displaystyle f_{X}(x)=\int _{-\infty }^{\infty }f_{XY}(x,y)\,\mathrm {d} y}$

Le rapport de la densité de probabilité jointe (relative à une valeur ${\displaystyle x\,}$) à la densité marginale de ${\displaystyle Y\,}$ (concernant toutes les valeurs ${\displaystyle x\,}$) représente la densité de probabilité conditionnelle de ${\displaystyle X\,}$ sous la condition ${\displaystyle Y=y\,}$ :

${\displaystyle f_{X|Y}(x,y)={\frac {f_{XY}(x,y)}{f_{Y}(y)}}}$

L'espérance mathématique d'une fonction ${\displaystyle g\,}$ de deux variables généralise la formule donnée pour une seule variable :

${\displaystyle \mathbb {E} [g(X,Y)]=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\ g(x,y)\,p_{XY}(x,y)\,\mathrm {d} x\,\mathrm {d} y}$

L'opérateur espérance est linéaire ; en particulier, l'espérance (la moyenne) d'une somme de deux variables aléatoires est la somme des moyennes :

${\displaystyle \mathbb {E} [X+Y]=\mathbb {E} [X]+\mathbb {E} [Y]\,}$

Parmi ces espérances, une double transformation de Fourier conduit à la fonction caractéristique:

${\displaystyle \varphi _{XY}(\theta ,\psi )=\mathbb {E} [e^{i(\theta X+\psi Y)}]}$

Comme pour le cas d'une seule variable aléatoire un développement en série permet de faire apparaître les moments que l'on peut centrer par soustraction des moyennes.

Si la densité de probabilité conditionnelle de ${\displaystyle X\,}$ par rapport à ${\displaystyle Y\,}$ est identique à la densité marginale :

${\displaystyle p_{X}(x)={\frac {p_{XY}(x,y)}{p_{Y}(y)}}}$

on dit que les deux variables sont indépendantes. L'égalité se réécrit :

${\displaystyle p_{XY}(x,y)=p_{X}(x)\,p_{Y}(y)\,}$

La fonction caractéristique de la somme des variables est alors égale au produit des fonctions caractéristiques individuelles :

${\displaystyle Z=X+Y\qquad \varphi _{Z}(\theta )=\varphi _{X}(\theta )\,\varphi _{Y}(\theta )}$

C'est l'une des principales propriétés de la fonction caractéristique. Cette remarque est, entre autres, utilisée dans la démonstration du théorème central limite.

On appelle corrélation de deux variables aléatoires la grandeur:

${\displaystyle \rho ={\frac {\mathbb {E} [(X-{\overline {X}})(Y-{\overline {Y}})]}{\sigma (X)\,\sigma (Y)}}}$

où ${\displaystyle \sigma (X)={\sqrt {\mathbb {E} [(X-{\overline {X}})^{2}]}}}$ est l'écart-type de la variable ${\displaystyle X}$. La corrélation de deux variables est comprise entre -1 et 1. Pour une corrélation proche de 1 la variable X aura tendance à être grande quand Y le sera et vice versa. Pour une corrélation proche de -1 la variable X aura tendance à être petite quand Y le sera grande. Si la covariance est nulle on dit que les deux variables sont décorrélées. La formule se développe alors en:

${\displaystyle \mathbb {E} [XY]=\mathbb {E} [X]\,\mathbb {E} [Y]\,}$

Si les deux variables sont indépendantes, elles sont décorrélées, l'inverse n'étant pas vrai, car l'indépendance implique tous les moments au lieu d'un seul. La notion de variables décorrélées est plus faible que celle d'indépendance et est loin d'avoir la même utilité.