FRACTRAN
FRACTRAN est un langage de programmation exotique et Turing-complet s'appliquant à des entiers naturels. Il a été inventé par le mathématicien John Conway qui en publie une description en 1987[1] - [note 1].
Un programme FRACTRAN est constitué par une liste ordonnée de fractions, et un nombre entier de départ. Le programme produit une suite d'entiers , définie par la procédure suivante :
- Initialiser l'examen avec la première fraction de la liste ;
- Si la multiplication donne un entier, cet entier sera (par définition) (et réinitialiser l'examen en 1 pour trouver son successeur) ;
- Sinon, si la liste des fractions n'est pas épuisée, poursuivre l'examen avec la fraction suivante (et reprendre l'examen en 2) ;
- Sinon la procédure s'arrête (et la suite résultat est alors finie).
Fonctionnement d'un programme FRACTRAN
Exemple
Considérons le programme FRACTRAN correspondant à la liste de fractions .
Si on l'applique à l'entier 14, comme ni , ni ne sont des entiers, le programme s'arrête immédiatement.
Si on l'applique à l'entier 15, on obtient successivement 20 (car seul est un entier), puis 6 (car est un entier) , puis 8 (car seul donne un entier), puis la procédure s'arrête.
Principe
Le principe s'appuie sur l'existence d'une décomposition en produits de facteurs premiers des entiers, et sur la notion de valuation p-adique.
Tout entier A possède une décomposition en produit de facteurs premiers unique, dans laquelle l'exposant du nombre premier p est appelé valuation de p dans A, et est noté . Pour un entier A donné, les sont tous nuls, sauf un nombre fini d'entre eux.
Un programme FRACTRAN peut être vu comme fonctionnant sur une machine disposant d'une infinité de registres, chaque registre contenant un nombre entier. L'état de la machine est alors donné par le codage de Gödel, où les registres successifs représentent l'exposant des nombres premiers successifs. Par exemple, l'état 60 est donné par sa décomposition en facteurs premiers :
Il représente l'état où le premier registre (celui de 2) contient la valeur 2, le second (celui de 3) contient la valeur 1, le troisième (celui de 5) contient la valeur 1, et tous les autres registres sont à zéro. Ou encore, en termes de valuation, v2=2, v3=1 et v5=1.
Multiplier l'entier A par une fraction N/D permettant d'obtenir un entier B, consiste à opérer, en parallèle sur l'ensemble des p, des additions et des soustractions sur les : la valuation de p dans A est augmentée de celle de p dans N, ou diminuée de celle de p dans D.
Analyse de l'exemple
Ainsi, la liste précédente (3/10, 4/5) n'opère que sur les valuations de 2, 3 et 5, qui sont les seuls facteurs premiers présents dans les deux fractions :
- La première fraction () enlève 1 aux valuations de 2 et 5, lorsque cela est possible, et dans ce cas augmente de 1 la valuation de 3. Cette première fraction agit donc tant que les valuations de 2 et de 5 sont strictement positives.
- La seconde fraction () ne prend le relai que lorsque la première ne peut plus opérer, c'est-à-dire quand la valuation de 2 ou de 5 est nulle. Dans ce cas, elle augmente la valuation de 2 de deux unités, et baisse celle de 5 d'une unité.
Lorsque A s'écrit (multiplié par un facteur A’ quelconque premier avec 30),
- si , avec la première fraction la procédure transforme A en , puis avec la seconde fraction transforme le résultat en , et la procédure s'arrête.
- si , le comportement de la suite est plus complexe :
- La première fraction donnera ;
- la seconde fraction prend le relai et transforme le résultat en .
- Si l'exposant de 5 n'est pas nul, la première fraction reprend la main pour donner , voire ;
- ... et ainsi de suite, les fractions alternant leur transformation jusqu'à ce que l'exposant de 5 soit nul.
Le « programme » que constitue la liste des fractions permet ainsi de définir des opérations sur les valuations.
Opérations basiques
Addition
La liste contenant l'unique fraction permet de faire la somme des valuations de 2 et de 3 : lorsque A s'écrit , la procédure s'applique jusqu'à ce que A soit transformé en .
Cette procédure met à zéro l'exposant de 2. Si l'on veut faire l'addition en préservant cette valeur, il est possible de le faire en deux temps :
- La fraction réalise l'addition sur 3 tout en transférant sur 5 la valuation de 2 ;
- La fraction restaure sur 2 la valuation originale.
Le programme (15/2 ; 2/5) transforme donc un nombre de la forme en s'arrêtant sur le résultat final . Noter que la valuation de 5 dans le nombre d'entrée est nécessairement nulle pour qu'il puisse servir de registre intermédiaire.
Soustraction
La simple fraction permet de transformer le nombre en
- , si ;
- , si ;
- si .
Boucle infinie
Les exemples précédents donnent des séries finies, mais ce n'est pas nécessairement le cas. Un programme simple comme (2/3 ; 3/2) appliqué à n'importe quel nombre d'entrée commencera dans un premier temps par transférer la valuation de 3 en l'additionnant à celle de 2.
À ce stade, si l'une ou l'autre des valuations n'est pas nulle au départ, le programme bouclera :
- Le registre des 3 étant épuisé, le programme ne peut appliquer [2/3] et appliquera [3/2], déplaçant une unité du registre des deux vers celui des 3.
- L'étape suivante, le registre des 3 contenant une unité, [2/3] s'appliquera en priorité, transférant l'unité en sens inverse.
Ce système de bouclage est cependant très utile pour gérer des boucles de programmes grâce à des couples d'indicateurs d'états, comme le montre l'exemple suivant de la multiplication.
Recopie d'un nombre
Il est souvent utile en programmation de transférer un nombre d'un registre à un autre, voire de le dupliquer.
Par exemple, le transfert du registre des 2 vers celui des 3 s'effectuera par la réitération de l'opération (3/2) ; et la duplication de ce dernier vers les registres des 2 et 5 se fera par la réitération de l'opération (10/3), qui remplit simultanément les registres des 2 et 5 en vidant le registre des 3.
Deux points importants sont à noter pour de telles opérations :
- Un transfert ne se fait (généralement) pas en une opération unique, mais à travers la réitération d'opérations élémentaires, transférant des quantités élémentaires. De ce fait, il faut garder en tête que sans autres précautions, la procédure permet que d'autres opérations sont susceptibles de s'intercaler pendant un transfert, lesquelles peuvent modifier ou compromettre le résultat.
- Il n'est pas possible de dupliquer directement un registre source en le recopiant vers un registre destination. Le transfert d'une source vers la destination épuisant le registre source en le mettant à zéro, une duplication doit nécessairement être précédée ou suivie d'un simple transfert. De ce fait, une duplication de registre mobilise nécessairement trois registres, et non deux.
Bien entendu, pour leur bon fonctionnement, ces opérations supposent que le registre d'accueil ou intermédiaire est initialement à zéro. Cette condition est normalement assurée en imposant des conditions au nombre de départ. Pour la multiplication décrite ci-après, par exemple, le transfert du produit des registres des 2 et des 3 vers celui des 5 nécessite l'utilisation d'un registre supplémentaire (assigné à celui des 7), pour réaliser des duplications, et deux autres (ceux des 11 et 13), pour réaliser un indicateur d'états.
L'algorithme par conséquent prend un nombre de la forme
...pour rendre un nombre de la forme
...et ne peut fonctionner que si initialement les registres des 5, 7, 11 et 13 sont à zéro (le reste étant indifférent).
Multiplication
On peut créer une fonction multiplicative à l'aide d'une boucle additive. L'idée centrale d'un tel algorithme est que partant d'un résultat nul, calculer consiste à additionner fois la valeur au résultat. Cet algorithme s'applique à un nombre et le transforme en .
En termes de registres, on peut coder par v2, par v3 et le résultat par v5. Fondamentalement, l'opération consiste à additionner v3 à v5, et répéter l'opération v2 fois.
- Restauration du registre v3
Comme l'addition de v3 à v5 « consomme » la valeur de v3, il nous faudra également un registre v7 pour mémoriser cette valeur et la restaurer d'une addition à l'autre. En notant les fractions qui réalisent les différents transferts, l'algorithme devient :
- [ 1/2 ] Si v2 n'est pas nul, le décrémenter (pour compter un passage) ;
- [ 5x7 / 3 ] Une boucle intérieure ajoute v3 à v5, et en parallèle, recopie aussi v3 en v7 (ce faisant, en mettant v3 à zéro) ;
- [ 3/7 ] Quand la boucle intérieure est terminée (v3 est nul), on remet v3 la valeur initiale (présente dans v7, ce faisant, mettant v7 à zéro).
- Puis on recommence (tant que v2 n'est pas nul).
- Etats successifs de l'algorithme
Cependant, on voit que la règle disant que les fractions sont examinées dans un ordre fixe ne permet pas simplement de recopier d'un côté v3 en v7, puis v7 en v3. La présence simultanée d'un facteur [7/3] et d'un facteur [3/7] dans la liste risque d'engendrer le même type de boucle infinie que précédemment. Suivant la fraction rencontrée en premier, l'une des opérations sera prioritaire sur l'autre, et l'un ou l'autre de ces deux registre ne pourra pas être vidé jusqu'au bout.
Pour retenir l'une des actions tant que l'autre n'est pas terminée, il faut introduire la notion d'état dans l'algorithme, et distinguer entre un état A, où v7 est transféré vers v3 pour le réinitialiser, et un état B, où l'addition de v3 à v5 est réalisée tout en transférant v3 à v7. L'algorithme devient :
| État courant | Étape | Condition | Action élémentaire | Opérateur | État suivant |
|---|---|---|---|---|---|
| A | Réinitialisation : transférer v7 à v3 | v7 > 0 | Soustraire1 à v7 ajouter 1 à v3 |
3/7 | A |
| Si v2 positif, décrément et entrée en boucle B |
v7 = 0 et v2 > 0 |
Soustraire 1 à v2 | 1/2 | B | |
| Vider v3 | v7 = 0 et v2 = 0 et v3 > 0 |
Soustraire 1 à v3 | 1/3 | A | |
| Fin du programme | v7 = 0 et v2 = 0 et v3 = 0 |
Stop (résultat dans v5) |
∅ | ∅ | |
| B | Ajouter v3 à v5 et v7 | v3 > 0 | Soustraire 1 à v3 Ajouter 1 à v5 Ajouter 1 à v7 |
5*7 / 3 | B |
| Réinitialiser | v3 = 0 | Rien | A |
- Indicateurs d'état couplés
Pour gérer ces états, de nouvelles variables sont nécessaires : elles jouent le rôle d'indicateurs d'états. L'idée de base est que si la valeur d'un indicateur (v11) est nulle dans l'état courant, toute fraction présentant cet indicateur au dénominateur ne pourra pas être exécutée. Cependant, deux indicateurs d'états sont nécessaires pour la seule boucle B : en effet, le premier indicateur (v11) étant consommé par le test, il est nécessaire d'en posséder un second (v13) pour indiquer au programme qu'il doit continuer dans le même état.
Les indicateurs d'état pour la boucle B seront donc v11 et v13.
- Tant que ces deux indicateurs sont nuls, les fractions de la boucle B (qui doivent donc être examinées en premier) ne peuvent pas s'exécuter, et les fractions de l'état A (qui sont examinées ensuite) sont exécutées.
- [ 3/7 ] v7 est retranscrit dans v3.
- [ 11/2 ] v2 décrémenté d'une unité, et v11 est positionné à 1, permettant l'exécution des éléments de la boucle B.
- [ (5.7.13) / (3.11) ] v3 est additionné à v5 et transféré à v7, si v11 le permet. Mais ce test « consommant » v11, il faut dupliquer provisoirement l'information dans v13.
- [ 11/13 ] L'indicateur v13 est ensuite retransféré en v11, permettant de répéter la boucle B. La présence simultanée des facteurs 11/13 et 13/11 créé une boucle dans l'état B, mais cette boucle n'est pas infinie, parce que v3 finit par s'annuler.
- [ 1/11 ] Quand le transfert est achevé, la boucle B doit s'interdire d'intervenir tant que la main est à l'état A, en repositionnant v11 à zéro.
En fin de comptes, l'algorithme travaille sur les valuations de 2, 3, 5 mais aussi 7, 11 et 13. En ajoutant les indicateurs d'états et les instructions associées au tableau d'algorithme de la multiplication, on obtient :
| Instruction FRACTRAN |
État courant | Indicateurs d'état |
Condition | Action | État suivant |
|---|---|---|---|---|---|
| A | Aucun | v7 > 0 | Soustraire 1 à v7 Ajouter 1 à v3 |
A | |
| v7 = 0 et v2 > 0 |
Soustraire 1 à v2 Mettre v11 à 1 |
B | |||
| v7 = 0 et v2 = 0 et v3 > 0 |
Soustraire 1 à v3 | A | |||
| v7 = 0 et v2 = 0 et v3 = 0 |
Stop | ||||
| B | v11, v13 | v3 > 0 | Soustraire 1 à v3 Ajouter 1 à v5 Ajouter 1 à v7 |
B | |
| v3 = 0 | Mettre v11 à 0 | A |
Quand on écrit la liste d'instructions FRACTRAN, on doit mettre les instructions de l'état A en dernier, car l'état A n'a pas d'indicateur d'état, c'est l'état par défaut. Tous les autres états, en effet (un seul dans cet exemple) sont protégés en exécution par leurs indicateurs d'état.
Ainsi le programme FRACTRAN de multiplication est la liste suivante :
Si on entre le nombre , le programme rend [note 2].
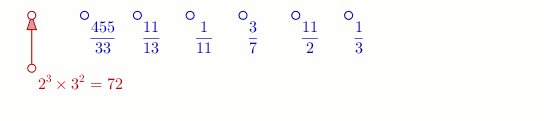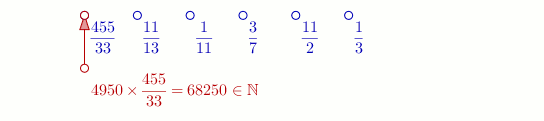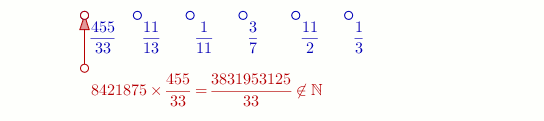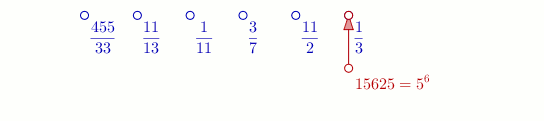
Division euclidienne
La division euclidienne de a par b (a et b entiers naturels, b > 1) est la donnée de deux entiers naturels q et r tels que r < b et a = bq + r. Cette division euclidienne peut être vue comme une boucle de soustractions : diviser a par b, c'est ôter b à a autant de fois qu'il est nécessaire, le nombre de fois où cette soustraction est effectuée correspond à q, la dernière valeur dans a correspond au reste.
L'algorithme travaille lors sur v2 contenant a, v3 contenant b, v5 destiné à contenir q, et v7 destiné à contenir r. Ces variables sont complétées par 4 indicateurs d'états v11, v13, v17, v19.
Le programme FRACTRAN qui suit consiste en trois états :
- l'état A opère différemment selon que v3 est plus petit ou plus grand que v2;
- si v3 ≤ v2, la boucle retranche v3 à v2, vide v3 dans v7, ajoute 1 à v5 et passe à l'état B ;
- si v3 > v2, la boucle vide v2 dans v7 et passe à l'état X.
- l'état B est une sur-boucle qui ré-effectue la boucle A après avoir au préalable vidé v7 dans v3;
- l'état X consiste à vider v3 quand v2 est vide et v3 est non vide.
| Instructions FRACTRAN |
État courant | Indicateurs d'état |
Conditions | Actions | État suivant |
|---|---|---|---|---|---|
| A | v11, v13 | v2 > 0 et v3 > 0 |
Soustraire 1 à v2 Soustraire 1 à v3 Ajouter 1 à v7 |
A | |
| v2 = 0 et v3 > 0 |
Soustraire 1 à v3 Mettre v11 à 0 |
X | |||
| v3 = 0 | Ajouter 1 à v5 Mettre v11 à 0 Mettre v17 à 1 |
B | |||
| B | v17, v19 | v7 > 0 | Soustraire 1 à v7 Ajouter 1 à v3 |
B | |
| v7 = 0 | Mettre v11 à 1 Mettre v17 à 0 |
A | |||
| X | v3 > 0 | Soustraire 1 à v3 | X | ||
| v3 = 0 | Stop |
L'écriture du programme est alors :
Il suffit d'entrer pour obtenir en sortie où avec .
Génération de suites
Certains programmes bouclent indéfiniment, et génèrent des suites infinies.
Algorithme de Conway des nombres premiers
Le programme suivant est présenté par John Conway dans le livre coécrit avec Richard Guy The Book of Numbers. John Conway les appelle « les 14 fractions fantastiques »[1].
Ce programme, appliqué à l'entier 2, génère une suite qui contient tous les termes de la forme où est un nombre premier. Réciproquement, toute puissance de 2 dans cette suite a pour exposant 1 ou un nombre premier. Cette suite porte le nom de Conway primegame[2].
L'algorithme est essentiellement un algorithme de division euclidienne. Le principe est le suivant : partant d'un nombre de la forme où 0 ≤ m < n, l'algorithme tente de diviser n+1 par tous les nombres de n à 1, jusqu'à ce qu'il trouve le plus grand entier k tel que k divise n+1 et retourne alors . Les seuls cas où l'algorithme rend une puissance de 2 sont les cas où k = 1, c'est-à-dire les cas où n+1 est premier[note 3].
Suite de Fibonacci
Le programme suivant :
appliqué à l'entier 3, génère une suite qui contient tous les termes de la forme où a et b sont deux termes consécutifs de la suite de Fibonacci. Réciproquement, tout terme de la suite de la forme a pour exposant deux termes consécutifs de la suite de Fibonacci.
L'algorithme est essentiellement un algorithme d'addition qui consiste, en partant de à fournir .
En effet :
- pour , la fraction transforme en , puis les fractions et transforment itérativement ce dernier en . Dans le cas où , on arrive directement à grâce au 7 final de la liste ;
- La fraction transforme alors en , puis les fractions et le transforment itérativement en ;
- La fraction le transforme en , puis les fractions et le transforment en ;
- Enfin, la fraction supprime le facteur 19.
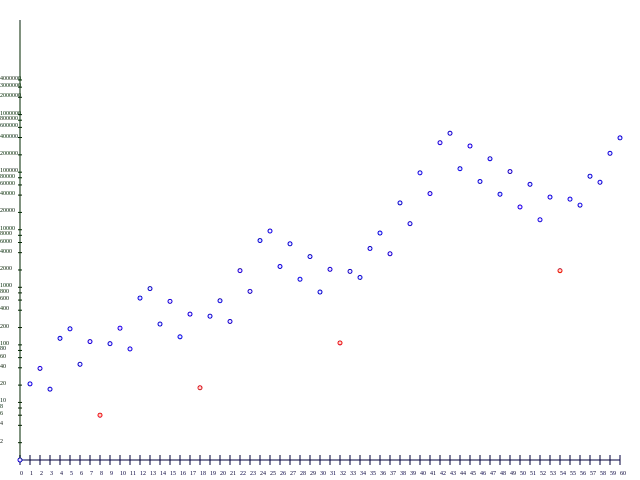
| Rang | Nombre | Facteurs premiers |
|---|---|---|
| 8 | 6 | |
| 18 | 18 | |
| 32 | 108 | |
| 54 | 1944 |
Suite de Syracuse
Ce programme présenté par Kenneth G. Monks[3] :
appliqué à , génère une suite qui contient successivement tous les termes , où b parcourt les termes de la suite de Syracuse de premier terme N. Réciproquement, toute puissance de 2 dans cette suite a pour exposant un élément de la suite de Syracuse.
- Partant de , les fractions et le transforme en pour les valeurs croissantes de k jusqu'à arriver à si N est pair égal à 2p, ou bien si N est impair égal à 2p+1.
- Dans le premier cas, le terme final 7 transforme en , puis les fractions et le transforment itérativement en . La fraction supprime ensuite le 7 superflu. On est alors passé de à .
- Dans le deuxième cas, la fraction transforme en , puis les fractions et le transforment itérativement en . La dernière fraction le transforme enfin en qui n'est autre que .
L'idée de Kenneth Monks est d'étudier les suites de Syracuse cycliques en cherchant les propriétés des suites cycliques générées par ce programme[3].
Programme universel
Conway a également défini un programme FRACTRAN universel[note 1], constitué des fractions suivantes :
On peut alors montrer que, pour toute fonction partielle récursive f, il existe un entier c tel que, pour tout entier n, en appliquant le programme FRACTRAN avec la liste ci-dessus au nombre , on atteint le nombre si et seulement si le calcul de f(n) se termine. Cette propriété montre qu'on obtient en FRACTRAN toutes les fonctions calculables.
Notes et références
Notes
- Dans l'article FRACTRAN: A simple universal programming language for arithmetic, paru dans le livre de Cover et Gopinath, Open Problems in Communication and Computation, Springer-Verlag, New York, (1987), p. 4-26.
- (en) Des algorithmes similaires sont décrits dans cette page.
- Pour une explication détaillée, voir Julian Havil, Nonplussed!: Mathematical Proof of Implausible Ideas, Princeton University Press, 2007, (ISBN 978-0691120560).
Références
- Julian Havil, Nonplussed!: Mathematical Proof of Implausible Ideas, p. 162-163.
- Voir suite A007542 de l'OEIS.
- (en) [PDF] Kenneth G. Monks, « 3x+1 minus the + », in Discrete Mathematics and Theoretical Computer Science 5, 2002, 47–54.
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « FRACTRAN » (voir la liste des auteurs).
Voir aussi
Articles connexes
Ressources bibliographiques
- John Conway, « FRACTRAN: A simple universal programming language for arithmetic », in Open Problems in Communication and Computation, Thomas M. Cover (relecteur), B. Gopinath (relecteur), Springer ; 1re éd. () ;
- Julian Havil, Nonplussed!: Mathematical Proof of Implausible Ideas, Princeton University Press, 2007 ;
- Kenneth G. Monks, « 3x+1 minus the + », in Discrete Mathematics and Theoretical Computer Science 5, 2002, 47–54.






















































































































