Espace régulier
En mathématiques, un espace régulier est[1] un espace topologique vérifiant les deux conditions de séparation suivantes[2] :
Propriété T3
Soit E un espace topologique (non nécessairement séparé). Les propositions suivantes sont équivalentes :
- E est T3 ;
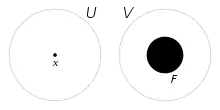
- on peut séparer un point x et un fermé ne contenant pas x par deux ouverts d'adhérences disjointes ;
- tout point x admet une base de voisinages fermés (autrement dit : tout ouvert contenant x contient un voisinage fermé de x)[1] ;
- tout fermé est l'intersection de ses voisinages fermés[3].
La topologie grossière (sur n'importe quel ensemble) est T3.
La propriété T3 est (de même que T2) préservée par sous-espaces et par produits.
Espace complètement régulier
Un espace topologique est dit complètement régulier s'il est uniformisable et séparé[4]. Tout espace complètement régulier est régulier, car un espace X est uniformisable si et seulement si pour tout point x de X et tout fermé F de X ne contenant pas x, il existe une fonction continue de X dans le segment [0, 1] valant 0 en x et 1 sur F.
Par exemple, tout groupe topologique séparé est complètement régulier. Les espaces normaux et les espaces localement compacts sont complètement réguliers.
Notes et références
- N. Bourbaki, Topologie générale, Chapitres 1 à 4, Berlin, Springer, (1re éd. 1971), 376 p. (ISBN 978-3-540-33936-6, lire en ligne), I.56.
- Ou simplement T0 et T3, puisque T0∧T3 ⇒ T2.
- (en) « A topological space is regular if and only if any closed set Z is the intersection of its closed neighborhoods? », sur math.stackexchange.
- N. Bourbaki, Topologie générale, Chapitres 5 à 10, Berlin, Heidelberg, Springer, (1re éd. 1974), 336 p. (ISBN 978-3-540-34486-5, lire en ligne), IX.8.
Article connexe
- Espace semi-régulier (en)