Escargot de Pythagore
L'escargot de Pythagore, « spirale de Théodore » ou encore « spirale d'Anderhub » est une figure qui permet de construire géométriquement les racines carrées des entiers consécutifs[1].
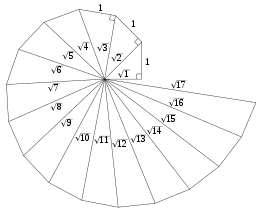
Construction
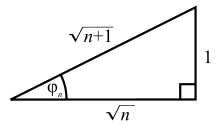
On part d'un triangle rectangle dont les côtés de l'angle droit sont de longueur 1. Par application du théorème de Pythagore, son hypoténuse a pour longueur .
Puis, à partir de l'hypoténuse de ce triangle, on construit un nouveau triangle rectangle : l'hypoténuse du premier triangle forme un des côtés de l'angle droit du nouveau triangle, l'autre côté de l'angle droit est à nouveau de longueur 1. En appliquant de nouveau le théorème de Pythagore, l'hypoténuse de ce second triangle rectangle a pour longueur tel que . On a donc . On peut alors réitérer la construction, en construisant à chaque fois un nouveau triangle rectangle dont un des côtés de l'angle droit est l'hypoténuse du triangle rectangle précédent, l'autre côté de l'angle droit ayant pour longueur 1. Les longueurs des hypoténuses des triangles rectangles ainsi obtenus sont les racines carrées des entiers consécutifs.
En généralisant ce principe, un triangle avec les côtés adjacents à l'angle droit de longueur et 1 a une hypoténuse de longueur .
Histoire
La première occurrence de cette construction remonte à Jakob Heinrich Anderhub, qui la surnomme « spirale de Théodore » en l'honneur de Théodore de Cyrène, qui aurait pu découvrir cette figure en son temps pour prouver l’irrationalité des racines carrées des nombres entiers non carrés jusqu'à 17[1].
Notes et références
- André Stoll, « Les spirales (1re partie) » [PDF], sur univ-irem.fr, (consulté le )





