Effet de cage

En chimie, l'effet de cage est un phénomène qui décrit comment les propriétés d'une molécule sont affectées par ce qui l'entoure. Introduit à l'origine par Franck et Rabinovitch[1] en 1934, l'effet de cage suggère qu'au lieu d'agir comme une entité individuelle, les molécules dans un solvant sont plutôt décrites comme une entité encapsulée[2] - [3]. Afin d'interagir avec d'autres molécules, la particule en cage doit se répandre hors de sa cage de solvant. La durée de vie classique d'une cage de solvant est de 10⁻¹¹ s[4].

Les radicaux libres dans un solvant peuvent potentiellement réagir avec un monomère au sein de la cage du solvant, ou bien diffuser à l'extérieur de la cage.

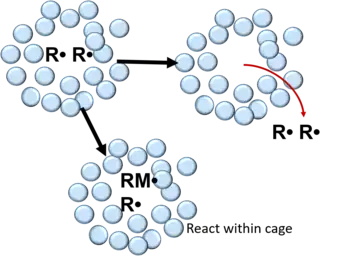
Lors de la polymérisation radicalaire, les radicaux libres formés lors de la décomposition d'un amorceur sont encerclés par une cage faite de solvant et/ou de monomères[3]. Au sein de cette cage, les radicaux subissent plusieurs collisions qui mènent à leur recombinaison ou bien une désactivation mutuelle[2] - [3] - [5]. Cela peut être décrit selon la réaction suivante[5] :

${\displaystyle {\text{R}}-{\text{R}}^{k_{1}}\rightleftharpoons _{k_{\text{c}}}\mathrm {R_{cage}} \centerdot ,\centerdot \mathrm {R_{paire}} \rightleftharpoons _{k_{\text{Dlibre}}}^{k_{\text{d}}}2{\text{R}}\centerdot _{\text{radicaux}}\rightarrow {\text{Produits}}}$

Après recombinaison, les radicaux peuvent soit réagir avec des monomères composant le pourtour de la cage ou bien diffuser librement hors de la cage. Pour les polymères, la probabilité qu'un radical s'apparie pour échapper à la recombinaison au sein de la cage est de l'ordre de 0,1 à 0,01 et de l'ordre de 0,3 à 0,8 dans les liquides[2].