Effet Bergeron
L’effet Bergeron, aussi appelé processus de nucléation de Wegener-Bergeron-Findeisen[1], est un processus de micro-physique des nuages en météorologie, décrit par Tor Bergeron en 1935, qui explique la croissance des cristaux de glace dans les nuages à des températures sous le point de congélation. À ces températures, la pression de surface des cristaux de glace est moindre que celle de l'eau liquide ce qui fait que les flocons de neige grossissent aux dépens des gouttelettes d'eau surfondues[2].
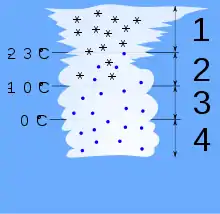
1) Cristaux de glace
2) Neige et gouttelettes surfondues (dominé par l'effet Bergeron)
3) Gouttelettes surfondues (dominé par la coalescence)
4) Gouttelettes de pluie
Histoire
Le principe de la croissance des cristaux de glace par déposition de vapeur d'eau atmosphérique aux dépens des gouttelettes de pluie surfondue fut formulé pour la première fois par le chercheur allemand Alfred Wegener en 1911. Il étudiait à l'époque la formation de la gelée blanche et théorisa que si le même processus se produisait dans les nuages, il pouvait mener à des flocons assez gros pour donner de la neige. Son travail sur la gelée attira immédiatement l'attention dans le milieu des chercheurs mais son extrapolation vers la production de flocons prit 10 ans avant d'y percer[3].
À l'hiver 1922, lors d'un séjour dans un spa à Voksenkollen près d'Oslo, Tor Bergeron fit une observation lors de nombreuses randonnées dans le bois environnant. Les jours où la température était sous le point de congélation et qu'une couche de stratus couvrait le ciel, la base du nuage ne descendait pas plus bas que la canopée. Cependant, les jours où la température était au-dessus de 0 °C dans les mêmes conditions, la base atteignait facilement le sol pour donner du brouillard[4]. Se rappelant l'hypothèse de Wegener, Bergeron supposa que les cristaux de glace formés sur les branches des arbres pouvaient cannibaliser les gouttelettes surfondues provenant du nuage, dissipant sa base[3] - [4].
En 1933, Bergeron assista à une réunion de l'Union géodésique et géophysique internationale à Lisbonne au Portugal et y présenta sa théorie. Dans son mémoire, il démontra que même une petite concentration de cristaux de glace dans un nuage de gouttelettes surfondues allait grossir aux dépens de ces dernières grâce à la différence de pression partielle de saturation des deux hydrométéores. Bergeron émit l'hypothèse que c'était le processus principal de production de pluie, même dans les climats tropicaux, ce qui causa alors une vive polémique entre les chercheurs en météorologie des latitudes moyennes et ceux des zones tropicales[3]. À la fin des années 1930, Walter Findeisen raffina l'hypothèse de Bergeron par des expériences et des explications théoriques[3].
Théorie
Dans l'atmosphère, la croissance la plus rapide des précipitations se produit dans la partie du nuage sous le point de congélation avec un maximum d'efficacité autour de -10 °C à -15 °C. À cette température, les trois phases de la molécule d'eau coexistent au sein de l'air : de la vapeur d'eau, des gouttelettes en surfusion et des cristaux de glace.
Partant de cette observation, Bergeron a proposé une explication du mécanisme de déclenchement des précipitations qui se fonde sur les différences entre les pressions de vapeur saturante de la vapeur d'eau par rapport à l'eau liquide, soit , et par rapport à la glace, soit . En effet, sous le point de congélation on a toujours[5] :
- .
Pour une pression partielle de la vapeur d'eau restant à peu près constante dans l'air environnant mais inférieure à , il y aura évaporation graduelle des gouttelettes. En même temps, sera lui saturé et l'excédent de vapeur d'eau ira se condenser sur les cristaux de glace pour garder l'équilibre de . L'effet Bergeron consiste ainsi en un transfert continuel de l'eau liquide des gouttelettes en surfusion vers l'eau solide des cristaux de glace au sein du nuage. Le poids des cristaux de glace finit alors par atteindre une valeur suffisante pour amorcer leur chute et donc les précipitations.
Effet similaire chez les gouttes
Un phénomène analogue à celui de l'effet Bergeron peut se produire, avec ou en l'absence de cristaux de glace, lorsque coexistent des gouttelettes sphériques de tailles nettement différentes. Ce phénomène est lié à la cohésion interne des gouttelettes à l'échelle microscopique. En effet, la diminution de rayon (R) d'une gouttelette à une température donnée a pour conséquence l'augmentation de sa tension de surface ce qui augmente la pression de vapeur saturante par rapport à elle. La valeur véritable est inversement proportionnelle à R et donc les plus grosses gouttelettes peuvent cannibaliser les plus petites comme les cristaux de glace le font des gouttelettes surfondues[2].
Coalescence
L’effet Bergeron semble bien adapté à la description de la plupart des "départs" de précipitations. Cependant, les valeurs pour atteindre un diamètre normal d'une goutte de pluie ou d'un cristal de neige sont trop longues, de l'ordre de quelques heures. On ne peut alors convenablement expliquer leur grossissement que par l'intervention d'un autre phénomène, la coalescence, qui provoque la collision et l'agglomération d'un très grand nombre de gouttelettes (éventuellement en surfusion) et de cristaux de glace (éventuellement fondus) au cours de leur chute[2] - [5].
Notes et références
- Occurrences en français de « Processus de nucléation de Findeisen-Bergeron », sur TERMIUM Plus, la banque de données terminologiques et linguistiques du gouvernement du Canada, (consulté le ).
- « Effet Bergeron », Météo-France (version du 16 septembre 2020 sur Internet Archive).
- (en) Kristine Harper, Weather and climate : decade by decade, Infobase Publishing, coll. « Twentieth-century science », , 250 p. (ISBN 978-0-8160-5535-7, lire en ligne), p. 71–77.
- (en) Robert Marc Friedman et David M. Schultz, « Bergeron, Tor Harold Percival », sur Encyclopedia.com (consulté le ).
- [Métavi] Service météorologique du Canada, MÉTAVI : L'atmosphère, le temps et la navigation aérienne, Environnement Canada, , 260 p. (lire en ligne [PDF]), chap. 10 (« Nuages, brouillards et précipitations »), p. 90-102.




