Distance lunaire

Distance Terre - Lune et phases lunaires en 2014. Phases de lune: 0 (1) – nouvelle Lune, 0,25 - premier quartier, 0,5 - pleine lune, 0.75 - dernier quartier.

Variation de la distance entre les centres de la Lune et la Terre pendant 700 jours.

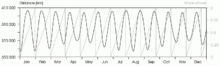
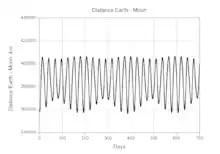
En raison de son orbite elliptique avec une excentricité variable, la distance instantanée varie avec une périodicité mensuelle. En outre, la distance est perturbée par les effets gravitationnels de divers corps célestes - la plus significative étant celle du Soleil et dans une moindre mesure celle de Jupiter. Les autres planètes du système solaire sont responsables de perturbations infimes de même que les astéroïdes, les forces de marée et les effets relativistes[10]. L'effet de la pression résultante de la radiation solaire contribue à produire des variations de ±3,6 mm de la distance lunaire[11].

La distance lunaire mesurée peut changer de plus de 21 000 km par rapport à la valeur moyenne tout au long d'un mois. Ces perturbations sont bien comprises[12] et la distance lunaire peut être modélisée avec précision sur des milliers d'années[10].

Le taux actuel de récession est de 3,805 ± 0,004 cm/an[12]. Il semble que ce taux ait augmenté récemment. En effet, une vitesse d’éloignement de 3,8 cm/an impliquerait que la Lune soit âgée de seulement 1,5 milliard d'années (Ga) alors que les scientifiques s’accordent autour d’un âge d’environ 4 Ga[13]. Il semble, de plus, que ce taux anormalement élevé d’éloignement continue à accélérer[14].

Les scientifiques envisagent que la distance lunaire continue à augmenter jusqu'à ce que la Terre et la Lune soient verrouillées gravitationnellement et aient une rotation synchrone. Cela se produit lorsque la durée de la période orbitale lunaire est égale à la période de rotation de la Terre. Les deux corps sont alors dans un équilibre et aucune autre énergie de rotation n’est échangée. Les modèles prédisent que 50 milliards d'années seraient nécessaires pour atteindre cette configuration[15].

La distance lunaire moyenne est en augmentation, ce qui implique que la Lune était plus proche dans le passé. Il existe des preuves géologiques que la distance lunaire moyenne était d'environ 52 R_⊕ (rayon terrestre) pendant l'ère précambrienne, soit il y 2,5 milliards d'années[13], contre environ 60 R_⊕ aujourd'hui.

L'hypothèse de l'impact géant, une théorie largement acceptée, affirme que la Lune a été créée à la suite d'un impact catastrophique entre une autre planète et la Terre entraînant une accumulation de fragments à une distance initiale de 3,8 R_⊕. D’après les estimations, l'impact initial est supposé avoir eu lieu il y a 4,5 milliards d'années[16].

La traction exercée par la lune sur la Terre ralentit également la rotation de la Terre, un effet connu sous le nom de freinage par effet de marée. Autrement exprimé, le moment angulaire est lentement transféré de la rotation de la Terre à l'orbite de la Lune. Ce ralentissement de la rotation se traduit par l’augmentation de la durée des jours (24 heures) de 2,3 millisecondes par siècle. L'énergie perdue par la Terre est transférée à la Lune qui augmente alors sa distance de la Terre à une vitesse de 3,8 centimètres par année[17]. La raison de ce transfert est que la rotation de la Terre provoque un entraînement de l'eau des océans déplacée par les marées ce qui déplace le centre de masse de la Terre, créant une accélération tangentielle sur la Lune, augmentant graduellement sa vitesse dans son orbite. Par conséquent, la vitesse de rotation de la Terre diminue imperceptiblement et la Lune accélérant sur son orbite, le rayon de celui-ci est progressivement en augmentation.

La méthode la plus ancienne de la détermination de la distance lunaire consiste à mesurer l'angle simultanément entre la Lune et un point de référence choisi parmi plusieurs emplacements. La synchronisation peut être coordonnée en effectuant des mesures à un moment prédéterminé ou lors d'un événement observable à toutes les parties. Avant l’apparition de chronomètres mécaniques précis, l'événement de synchronisation était généralement une éclipse lunaire ou le moment où la lune traversait le méridien (si les observateurs ont partagé la même longitude). Cette technique de mesure est connue sous le nom de parallaxe lunaire.

Pour une précision accrue, certaines erreurs systématiques doivent être prises en compte telles que la correction de l'angle mesuré pour tenir compte de la réfraction et de distorsion de la lumière à travers l'atmosphère.

Éclipse lunaire.

Les premières tentatives de mesure de la distance entre la Terre et la Lune exploitèrent les observations d'éclipse lunaire en se fondant sur la connaissance du rayon de la Terre et l’éloignement plus important du Soleil que celui de la Lune. En observant la géométrie d'une éclipse lunaire, la distance lunaire peut être calculée en utilisant la trigonométrie.

Le premier compte rendu d'une tentative de mesure de la distance à la Lune en utilisant la trigonométrie a été réalisé par l'astronome et mathématicien grec du IV^e siècle av. J.-C., Aristarque de Samos[21] puis, plus tard, par Hipparque dont les calculs produisirent un résultat de 59-67 R⊕[22]. Cette dernière méthode a été reprise dans les travaux de Ptolémée[23], qui a calculé une distance de 64 1/6 R⊕ à son point le plus éloigné[24] - [25].

Une expédition menée par l'astronome d'origine française A.C.D Crommelin a permis d’observer le transit méridional de la Lune la même nuit à partir de deux endroits différents (le moment où la Lune traverse un cercle imaginaire passant directement au-dessus et à travers les pôles). D’autres mesures précises de 1905 à 1910 ont mesuré l'angle d'élévation au moment où un cratère lunaire spécifique (Mösting A) franchissait le méridien à partir des stations de Greenwich et au cap de Bonne-Espérance qui sont situés à peu près à la même longitude[26]. La distance a ensuite été calculée avec une incertitude de ± 30 km et est restée la valeur de distance lunaire de référence pour le demi-siècle suivant.

En enregistrant, à partir de plusieurs emplacements de distance de séparation connue, l'instant où la Lune occulte une étoile en arrière-plan ou encore en mesurant l’angle entre la Lune et une étoile d'arrière-plan à un moment prédéterminé, la distance lunaire peut être calculée.

Les astronomes O'Keefe et Anderson ont calculé la distance lunaire en observant quatre occultations de neuf sites en 1952[27]. Ils ont calculé une distance moyenne de 381 504,6 ± 4,7 km puis la valeur a été affinée en 1962 par Irene Fischer, qui a incorporé des données géodésiques plus précises (données géométriques de la Terre) pour produire une valeur de 381 500,2 ± 0,2 km[26].

Une expérience menée en 1957 par le laboratoire de recherche naval américain a utilisé l'écho de signaux radar pour déterminer la distance Terre-Lune. Des impulsions radars d’une durée de 2 ms ont été diffusées à partir d'une antenne radio de plus de 15 mètres de diamètre. L’écho des ondes radio sur la surface de la Lune a été enregistré et le temps de parcours de l’onde mesuré. À partir de cette mesure, la distance a pu être calculée. En pratique, cependant, il était difficile d’obtenir un signal suffisamment clair (sans ondes parasites) pour qu'une mesure précise puisse être produite de façon fiable[28].

L'expérience a été répétée en 1958 au Royal Radar Establishment en Angleterre. Des impulsions radar d'une durée de 5 µs ont été transmises avec une puissance de crête de deux mégawatts à un taux de 260 impulsions par seconde. Comme pour l’expérience précédente, l’écho des ondes radio sur la surface de la Lune a été enregistré et le temps de parcours de l’onde mesuré. Plusieurs mesures ont été additionnées pour pouvoir obtenir un signal plus fiable en superposant notamment les traces de l'oscilloscope sur un film photographique. À partir de ces mesures, la distance a pu être calculée avec une incertitude de seulement 1,25 km[29].

Ces premières expériences ont été conçues comme des expériences de validation de concept et n'ont duré un jour. Leur suivi a duré un mois pour produire une valeur moyenne de 384 402 ± 1,2 km[30], mesure la plus précise de la distance lunaire à l'époque.

La mesure du temps nécessaire à un faisceau laser pour effectuer l'aller-retour après s’être reflechi directement sur la surface de la Lune a été réalisée pour la première fois en 1962 par une équipe du Massachusetts Institute of Technology et une équipe soviétique de l'Observatoire d'astrophysique de Crimée[31].

Réflecteur sur la surface de la Lune en 1969.

Au cours des missions Apollo en 1969, les astronautes ont placé des rétro-réflecteurs sur la surface de la Lune dans le but d'affiner la précision de cette technique de mesure. Les mesures actuelles utilisent toujours cet équipement et impliquent de multiples installations laser autour du monde. La précision instantanée des expériences du Ranging Lunar Laser permet d’atteindre une résolution inférieure au millimètre et est, à ce jour, la méthode la plus fiable pour déterminer la distance lunaire.

En raison de l'accessibilité contemporaine aisée à des dispositifs précis de synchronisation, des caméras numériques haute résolution, des récepteurs GPS, des ordinateurs puissants et de dispositifs de communication quasi instantanés, il est devenu possible pour les astronomes amateurs de réaliser des mesures de haute précision de la distance lunaire.

Par exemple, le 23 mai 2007, des photographies numériques de la Lune pendant la quasi-occultation de Regulus ont été prises à partir de deux localisations situées en Grèce et en Angleterre. En mesurant la parallaxe entre la lune et une étoile d'arrière-plan, la distance lunaire pouvait être calculée[32].

Un projet plus ambitieux appelé la « Campagne Aristarque », en référence à l’astronome antique grec, a été réalisée au cours de l'éclipse lunaire du 15 avril 2014[9].

• Marie-Christine de la Souchère, « La distance Terre-Lune au millimètre près », La Recherche, vol. 548,‎ juin 2019, p. 58-61 (lire en ligne)
• (en) Mohammad Farhat, Pierre Auclair-Desrotour, Gwenaël Boué et Jacques Laskar, « The resonant tidal evolution of the Earth-Moon distance », Astronomy & Astrophysics, vol. 665,‎ septembre 2022, p. 1-20, article n^o L1 (DOI 10.1051/0004-6361/202243445 )

• Orbite de la Lune
• Lunar Laser Ranging Experiment
• Unité astronomique
• Éphémérides
• Les Tables pruténiques d'Erasmus Reinhold
• Super lune