Dimension bipartie

Considérons un graphe G = (V, E) qui s'avère être biparti. Voici un exemple de couverture sous-graphes bipartis complets de G :

• Exemple de couverture par sous-graphes bipartis complets
• 
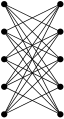  Un graphe G biparti
• 
  ... et une couverture par quatre sous-graphes bipartis complets
• 
  1. Le sous-graphe biparti complet rouge
• 
  2. Le sous-graphe biparti complet bleu
• 
  3. Le sous-graphe biparti complet vert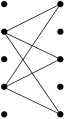
• 
  4. Le sous-graphe biparti complet noir

• La dimension bipartie d'un graphe complet ${\displaystyle K_{n}}$ est ${\displaystyle \lceil \log _{2}n\rceil }$.

• La dimension bipartie d'un graphe couronne à 2n sommets est ${\displaystyle \sigma (n)}$, où: ${\displaystyle \sigma (n)=\min \left\{\,k\mid n\leq {\binom {k}{\lfloor k/2\rfloor }}\,\right\}}$[1]

• La dimension bipartie d'un graphe grille de taille ${\displaystyle n\times m}$ est ${\displaystyle {\frac {nm}{2}}-1}$ si ${\displaystyle m}$ est pair et ${\displaystyle n-1=k(m-1)+2\ell }$ pour deux entiers ${\displaystyle 0\leq l<k}$ et est${\displaystyle {\big \lfloor }{\frac {nm}{2}}{\big \rfloor }}$ sinon[2].

• La dimension bipartie de nombreux graphes particuliers a déjà été déterminée : par exemple, pour le chemin ${\displaystyle P_{n}}$, ${\displaystyle d(P_{n})=\lfloor n/2\rfloor }$ et pour le cycle ${\displaystyle C_{n}}$, ${\displaystyle d(C_{n})=\lceil n/2\rceil }$[3].

Le calcul de la dimension bipartie d'un graphe G donné est un problème d'optimisation. Le problème de décision associé à la dimension bipartie peut être formulé ainsi :

Entrée : Un graphe ${\displaystyle G=(V,E)}$ non orienté et un entier positif ${\displaystyle k}$.

Sortie : Oui, s'il existe une couverture de G par sous-graphes bipartis complets de cardinal inférieur à ${\displaystyle k}$ ; non sinon.

Ce problème est appelé problème GT18 dans le livre de Garey et Johnson sur les problèmes NP-complets, et est une reformulation d'un autre problème sur les familles d'ensembles finis, le problème Set Basis nommé SP7.

Il a été prouvé que le problème GT18 est NP-complet[4], et ce même pour les graphes bipartis. Il reste NP-dur si l'on se restreint aux graphes dont la dimension bipartie est au pire en ${\displaystyle O(\log \,\!n)}$, avec n la taille de l'instance[5].

De plus, si P ≠ NP, ce problème ne peut être approximé finement : même pour les graphes bipartis, pour ${\displaystyle \epsilon >0}$ fixé, on ne peut pas approximer à plus de ${\displaystyle |V|^{1/3-\epsilon }}$[6]. Cependant, on peut montrer grâce à de la kernelisation que ce problème est FPT[7]. Ainsi, pour un graphe biparti à n sommets donné, on peut décider en ${\displaystyle O(f(k))+n^{3}}$, avec ${\displaystyle f(k)=2^{k2^{k-1}+3k}}$ si sa dimension bipartie est inférieure ou égal à ${\displaystyle k}$[8].

Le calcul de la dimension bipartie d'un graphe peut être utile dans différents contextes. Dans des systèmes informatiques, différents utilisateurs peuvent avoir accès à différentes ressources. Dans un système à Contrôle d'accès à base de rôles, un rôle donne les droits accès à certaines ressources. Un utilisateur peut avoir plusieurs rôles, et doit avoir accès à toutes les ressources liées à chacun de ses rôles. De plus, plusieurs utilisateurs peuvent avoir le même rôle. Le role mining problem consiste à trouver le nombre minimum de rôles, tels que chaque utilisateur a accès à des ressources spécifiques. L'ensemble des utilisateurs, combiné avec l'ensemble des ressources, forme un graphe biparti dont les arêtes sont les permissions. Tout sous-graphes bipartis complets est un rôle potentiel, et la solution du role mining problem est justement une couverture par sous-graphes bipartis complets minimale[9].

Un scénario similaire se rencontre en sécurité des systèmes d'information, plus précisément en sécurité de télédiffusion. Dans ce cas-là, plusieurs messages doivent être envoyés à certains ensembles de destinataires, via un moyen de communication non sécurisé. Chaque message doit être codé à partir d'une clé connue uniquement des destinataires. Chacun d'entre eux peut avoir plusieurs clés, et chaque clés peut être possédée par plusieurs destinataires. L'optimum key generation problem consiste à trouver un nombre minimal de clé pour que chaque transmissions soit sécurisé. Ce problème peut être modélisé par un graphe biparti, dont la couverture par sous-graphes bipartis complets minimale correspond à une solution du problème[10].

• Liste de problèmes NP-complets
• Couverture par sous-graphes bipartis complets
• Intersection number (graph theory) (en)

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Bipartite dimension » (voir la liste des auteurs).