Dilatance
Le phénomène de dilatance d'un sol décrit la variation de volume que l'on observe dans les matériaux granulaires lorsqu'ils sont soumis à un cisaillement[1] - [2]. Cet effet a été décrit scientifiquement pour la première fois par Osborne Reynolds en 1885-86[3] - [4].
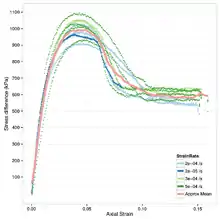
Contrairement à la plupart des autres matériaux solides, un matériau granulaire compacté tend à se dilater (à s'expandre en volume) lorsqu'on le cisaille. Cela vient de l'enchevêtrement des grains à l'état compacté : ces grains n'ont donc pas la possibilité de se réarranger par simple glissement. Lorsque l'amas de grains est chargé, il se produit un phénomène d'arc-boutement entre grains voisins, qui produit une expansion de l'échantillon. D'un autre côté, lorsque l'on comprime un matériau granulaire initialement lâche, il commence par se compacter au lieu de se dilater sous cisaillement. Un matériau granulaire est dit dilatant si son volume augmente sous cisaillement croissant, et contractant si son volume décroît lorsque le cisaillement augmente[5] - [6].
La dilatance est une propriété commune aux sols et aux sables. On peut en voir la manifestation aux traces qu'on laisse en marchant dans le sable. L'empreinte s'élargit au gré du séchage et l'eau interstitielle vient combler l'espace entre les grains de sable.
La dilatance est un objet d'étude pour les rhéologues, mais fait partie du champ plus général de la mécanique des sols.
Description
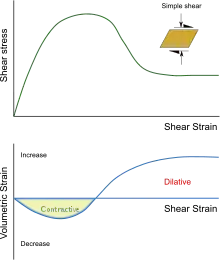
On peut observer le phénomène de dilatance dans un essai de cisaillement simple sur un échantillon de sable dense. Dans les premiers stades de la déformation, la distorsion fait décroître la variation relative de volume ; mais lorsque la contrainte approche de sa valeur de pic, la variation relative de volume ré-augmente. En poussant le cisaillement suffisamment loin, l'échantillon de sol finit par occuper un volume supérieure à celui qu'il occupait initialement.
L'augmentation relative de volume dépend beaucoup de la densité du sol : en général, plus l'échantillon de sol est dense, plus la variation de volume est sensible au cisaillement. Il a également été observé que l’angle de frottement interne diminue en même temps que la contrainte normale effective[7].
La relation entre dilatance et frottement interne est parfois présentée de façon imagée par le modèle « dents de scie », où l'angle de dilatance est analogue à l’angle des dents avec l’horizontale. Sur la base d'un tel modèle, on peut montrer que pour un sol non-dilatant, l’angle de frottement interne apparent est égal à l’angle de dilatance plus l’angle de frottement.
Intérêt du concept
La dilatance explique que l'angle de frottement interne augmente avec le taux de confinement d'un sol, jusqu'à atteindre un maximum (valeur de pic), mais décroît brutalement ensuite : cet effondrement du frottement interne des sables dilatants doit absolument être pris en compte dans les ouvrages (talus, piles et fondations ou tunnels).
Notes
- D'après R.M. Nedderman, Statics and kinematics of granular materials, Cambridge, UK, Cambridge University Press, , Digitally printed 1st pbk. version. éd., 372 p. (ISBN 0-521-01907-9, lire en ligne)
- Bruno Pouliquen, Joël Andreotti et Forterre, Granular media : between fluid and solid, Cambridge, Cambridge University Press, , 462 p. (ISBN 978-1-107-03479-2, lire en ligne)
- D'après Osborne Reynolds, « LVII. On the dilatancy of media composed of rigid particles in contact, with experimental illustrations », Philosophical Magazine Series 5, vol. 20, no 127, , p. 469–481 (DOI 10.1080/14786448508627791)
- D'après Osborne Reynolds, « Experiments showing dilatancy, a property of granular material, possibly connected with gravitation », Proc. Royal Institution of Great Britain, Read, .
- D'après A.Casagrande, R. C. Hirschfeld et S. J. Poulos, Fourth Report : Investigation of Stress-Deformation and Strength Characteristics of Compacted Clays, Cambridge (Massachusetts), HAarvard Univ. Press, coll. « Soil Mechanics Lab », .
- Poulos, S. J. (1971). The stress-strain curves of soils. Geotechnical Engineers Incorporated. Chicago.
- Cf. G. T.Houlsby, « How the dilatancy of soils affects their behaviour », sur University of Oxford, Department of Engineering Science,