Critère de planarité de Whitney
En mathématiques, et plus particulièrement en théorie des graphes, le critère de planarité de Whitney est une caractérisation, en théorie des matroïdes, des graphes planaires ; critère nommée d'après Hassler Whitney[1]. Il affirme qu'un graphe G est planaire si et seulement si son matroïde graphique est également cographique (c'est-à-dire qu'il est le matroïde dual d'un autre matroïde graphique).
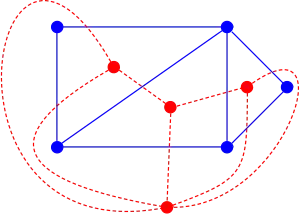
En termes de théorie des graphes pures, ce critère énonce comme suit :
- Un graphe est planaire si et seulement s'il existe un autre graphe , appelé le dual, et une correspondance bijective entre et telle qu'un sous-ensemble de forme un arbre couvrant de si et seulement si les arêtes correspondantes au sous-ensemble complémentaire forment un arbre couvrant de .
Dual algébrique
Une formulation équivalente du critère de Whitney est :
- Un graphe G est planaire si et seulement s'il a un graphe dual dont le matroïde graphique est dual du matroïde graphique de G.
Un graphe dont le matroïde graphique est le dual du matroïde graphique de G est appelé dual algébrique de G. Ainsi, le critère de planarité de Whitney peut être exprimé simplement comme suit[2] :
- Un graphe est planaire si et seulement s'il possède un dual algébrique.
Dual topologique
Si un graphe G est plongé dans une surface topologique telle que le plan, de sorte que chaque face du plongement est un disque topologique, le dual graphique du plongement est défini comme le graphe (ou dans certains cas le multigraphe) H qui a un sommet pour chaque face du plongement de G et une arête pour chaque paire de faces adjacentes. Selon le critère de Whitney, les conditions suivantes sont équivalentes :
- La surface sur laquelle le plongement existe est topologiquement équivalente au plan, à la sphère ou à la sphère trouée ;
- H est un dual algébrique de G ;
- chaque cycle simple de G correspond à une coupe minimale de H, et vice versa ;
- chaque cycle simple de H correspond à une coupe minimale de G, et vice versa ;
- chaque arbre couvrant de G correspond au complément d'un arbre couvrant de H, et vice versa[3].
Il est possible de définir des graphes duaux de graphes plongés sur des surfaces non planes telles que le tore, mais ces duaux ne vérifient en général pas la correspondance entre coupes, cycles et arbres couvrant requis par le critère de Whitney.
Références
- Hassler Whitney, « Non-separable and planar graphs », Transactions of the American Mathematical Society, vol. 34, no 2, , p. 339–362 (DOI 10.1090/S0002-9947-1932-1501641-2).
- Reinhard Diestel, Graph Theory, Springer-Verlag, coll. « Graduate Texts in Mathematics » (no 173), , 5e éd., 448 p. (ISBN 978-3-662-53622-3, lire en ligne), Theorem 4.6.3, p.113.
- W. T. Tutte, « Lectures on matroids », Journal of Research of the National Bureau of Standards, vol. 69B, , p. 1–47 (DOI 10.6028/jres.069b.001, MR 0179781, lire en ligne). Passages section 2.5, « Bon-matroid of a graph », p. 5–6, section 5.6, « Graphic and co-graphic matroids », p. 19–20, et section 9, « Graphic matroids », p. 38–47.







