Constante de Meissel-Mertens

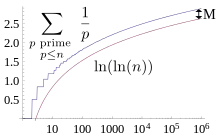
Soit ${\displaystyle S_{n}=\sum _{p\leqslant n}{\frac {1}{p}}}$ la somme des inverses des nombres premiers inférieurs ou égaux à ${\displaystyle n}$. La constante de Meissel-Mertens ${\displaystyle M}$ est définie par :

${\displaystyle M=\lim _{n\to \infty }\left(S_{n}-\ln(\ln n)\right)}$.

La série des inverses des nombres premiers diverge, tout comme la suite de terme général ${\displaystyle \ln(\ln n)}$ ; l'existence de cette constante indique que les deux expressions sont asymptotiquement liées :

${\displaystyle \sum _{p\leq n}{\frac {1}{p}}=\ln(\ln n)+M+o(1)}$ (où ${\displaystyle o(1)}$ est une notation de Landau).

La constante de Meissel-Mertens est reliée à la constante d'Euler-Mascheroni ${\displaystyle \gamma }$ (qui possède une définition similaire impliquant la différence entre la somme des inverses de tous les entiers de 1 à n et le logarithme népérien de n) par la formule suivante[1] - [2]:

${\displaystyle M=\gamma +\sum _{p{\text{ premier}}}\left(\ln \left(1-{\frac {1}{p}}\right)+{\frac {1}{p}}\right)}$.

Le fait qu'il existe deux logarithmes népériens (ln de ln) dans la limite pour la définition de la constante de Meissel-Mertens peut être perçu comme une conséquence de la combinaison du théorème des nombres premiers et de la limite définissant la constante d'Euler-Mascheroni.

La constante de Meissel-Mertens vaut approximativement 0,261497[3].