Conclusion répugnante

Parfit considère les quatre populations représentées dans le diagramme suivant : A, A+, B− et B. Chaque barre représente un groupe distinct de personnes, la taille du groupe est représentée par la largeur de la barre et le bonheur de chacun des membres du groupe est représenté par sa hauteur. Contrairement à A et B, A+ et B- comprennent deux groupes de personnes distincts. Parfit fait l'hypothèse que les vies des membres de chaque population sont suffisamment bonnes pour qu'il soit meilleure pour elle d'exister que de ne pas exister.

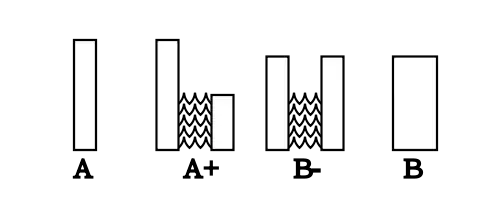
Comment ces populations se comparent-elles en valeur ?

Pour répondre à cette question, Parfit fait les quatre remarques suivantes :

• i) A+ ne semble pas pire que A. En effet, les personnes existant dans A+ et ayant des contreparties dans A ne sont pas moins bien loties dans A+ que leurs contreparties dans A tandis que les personnes supplémentaires existant dans A+ y sont mieux loties que dans A (en raison de l'hypothèse que leurs vies sont assez bonnes pour les préférer à la non existence).

• ii) B− semble mieux que A+. En effet, B− a un bonheur total et moyen supérieur à celui de A+.

• iii) B semble aussi bon que B−, la seule différence entre B− et B étant que les deux groupes de B- sont fusionnés pour former un unique groupe B.

Conjointement, ces trois comparaisons impliquent que B est meilleur que A.

• iv) Cependant, il semble que B peut être pire que A si on compare directement A et B. En effet, A est une population avec un bonheur moyen élevé tandis que B est une population avec un bonheur moyen inférieur, mais un bonheur total plus élevé en raison de sa population plus importante.

Il y a donc un paradoxe. Les affirmations suivantes, plausibles intuitivement, sont conjointement incompatibles : (i) A+ n'est pas pire que A, (ii) B- est mieux que A+, (iii) B- est aussi bon que B, et (iv) B peut être pire que A.

Certains chercheurs, tels que Larry Temkin et Stuart Rachels, soutiennent que l’incohérence apparente entre les quatre comparaisons repose sur l’hypothèse que la relation "meilleur que" est transitive. Nous pouvons résoudre l'incohérence en rejetant cette hypothèse. Avec ce point de vue, les faits que A+ n’est pas pire que A et que B− est meilleur que A+, n'impliquent pas que B− est meilleur que A.

Torbjörn Tännsjö soutient que l'intuition selon laquelle B est pire que A est fausse. Bien que la vie des personnes de B soit pire que celle de A, il y en a plus et la valeur collective de B est donc supérieure à A[1]. Michael Huemer affirme également que la conclusion répugnante n'est pas répugnante et que l'intuition normale est erronée.

Cependant, Parfit soutient que la discussion ci-dessus n'arrive pas à pointer la véritable source de répugnance. Supposons B supérieur à A comme le soutient Huemer. Cette intuition révisée doit être conservée dans les itérations suivantes. La prochaine itération ajouterait encore plus de personnes à B +, puis prendrait la moyenne du bonheur total, aboutissant à C-. Si ces étapes se répètent encore et encore, le résultat final sera Z, une population massive avec le niveau de bonheur moyen minimal. Ce serait une population dans laquelle chaque membre mènerait une vie extrêmement malheureuse. Parfit affirme que Z est la conclusion répugnante[2].

Un autre usage du terme « paradoxe de la simple addition» fut présenté dans un article de Hassoun en 2010[3]. Il présente le raisonnement paradoxal qui se produit lorsque certaines mesures statistiques sont utilisées pour calculer les résultats sur une population. Par exemple, si un groupe de 100 personnes possèdent ensemble 100 dollars, la richesse moyenne par habitant est de 1 dollar. Si une seule personne riche arrive avec 1 million de dollars, le groupe total de 101 personnes contrôle 1 000 100 $, soit une richesse moyenne de 9 901 $ par habitant, ce qui implique une réduction radicale de la pauvreté alors même que rien n’a changé pour les 100 premiers habitants. Hassoun définit un axiome appelé non simple addition pour juger de telles mesures statistiques : "le simple ajout d'une personne riche à une population ne devrait pas réduire la pauvreté" (tout en reconnaissant que, dans la pratique, l'ajout de personnes riches à une population peut procurer des avantages à l'ensemble de la population).

Ce même argument peut être généralisé à de nombreux cas où des statistiques proportionnelles sont utilisées. Par exemple, admettons qu'un jeu vendu sur un service de téléchargement soit considéré comme un échec si moins de 20% de ceux qui en téléchargent une démo gratuite achètent ensuite le jeu. Si 10 000 personnes téléchargent la démo et 2 000 l’achètent, le jeu est à peine un succès. Toutefois, le jeu basculerait dans la catégorie échec si 500 personnes supplémentaires téléchargeaient la démo sans acheter, même si cette "simple addition" ne change en rien le revenu ou la satisfaction du consommateur par rapport à la situation précédente.