Complexe de Čech
En topologie algébrique et en analyse topologique des données (en), le complexe de Čech est un complexe simplicial abstrait construit à partir d'un ensemble de points dans un espace métrique. Il est nommé d'après le mathématicien tchécoslovaque Eduard Čech.
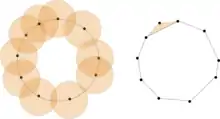
Complexe de Čech d'un ensemble de points disposés sur un cercle.
Étant donnés un ensemble fini de points et , le complexe de Čech est défini comme l'ensemble des simplexes tels que les boules de rayon et de centres les points de ont une intersection non vide, c'est-à-dire[1] :
Il peut être vu comme le nerf de l'ensemble des boules de rayon centrées sur les points de . Par le théorème du nerf, le complexe de Čech est homotopiquement équivalent à l'union des boules[1].
Le complexe de Čech est un sous-complexe du complexe de Vietoris–Rips.
Notes et références
- (en) Herbert Edelsbrunner et John Harer, Computational Topology: An Introduction, American Mathematical Soc., (ISBN 978-0-8218-4925-5, lire en ligne), p. 69-70
Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.






