Complémentaire (triangle)
En géométrie du triangle, on appelle point complémentaire d'un point par rapport à un triangle ABC, l'image du point par homothétie de centre, le centre de gravité de ABC et de rapport -1/2. Par extension, toute figure image par une telle homothétie sera appelée complémentaire.
Historique
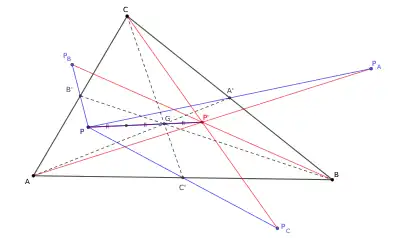
Dans le développement de la géométrie moderne du triangle, Nagel remarque l'existence de plusieurs triplets de centres du triangle alignés avec le centre de gravité et dans un rapport de distance de 2:1[1] - [2], travaux repris et étendus par Reuschle (en)[3].
En 1882, Maurice d'Ocagne découvre une construction des couples de points en considérant un point et son symétrique par rapport aux sommets du triangle médian du triangle de référence. En 1884, Émile Hain, revisitant la relation de conjugaison en prenant pour exemple un sommet d'un triangle et le milieu du côté opposé, observe que celui-ci est le sommet correspondant du triangle médian. En conséquence, il préfère envisager cette relation de conjugaison sous l'aspect de la complémentarité. Ainsi, ce centre devient le point complémentaire du sommet correspondant et par extension, P', le complémentaire de P. En 1886, Gaston Albert Gohierre de Longchamps considère la relation réciproque, qu'on appelle donc anticomplémentaire. L'année suivante, Émile Vigarié, un géomètre aveyronnais, est apparemment le premier à formuler cette complémentarité dans le langage vectoriel[4]. Plus tard, Adolphe Mineur, un professeur de l'université de Bruxelles, écrit en 1924 un livre sur les cubiques du triangle, où il expose une extension du concept de complémentarité algébriquement en recourant aux coordonnées barycentriques et trilinéaires[5].
Exemples
- Points
| Centre du triangle | Point complémentaire |
|---|---|
| Centre du cercle inscrit | Centre de Spieker |
| Centre de gravité | Centre de gravité |
| Centre du cercle circonscrit | Centre du cercle d'Euler |
| Orthocentre | Centre du cercle circonscrit |
| Point de Gergonne | Mittenpunkt |
| Point de Nagel | Centre du cercle inscrit |
| Point de Longchamps | Orthocentre |
| Coordonnées trilinéaires α : β : γ | Coordonnées trilinéaires bβ + cγa : aα + cγb : aα + bβc |
- Droites
- la droite complémentaire de la droite de Longchamps est l'axe orthique
- toute droite passant par le centre de gravité est sa propre complémentaire, comme la droite d'Euler ou la droite de Nagel, mais aussi la droite à l'infini
- Cercles
- le complémentaire du cercle circonscrit est le cercle d'Euler
- le complémentaire du cercle polaire est le cercle de de Longchamps
- Autres
- Le triangle complémentaire du triangle de base est son triangle médian
- Le complémentaire de l'ellipse circonscrite de Steiner est son ellipse inscrite de Steiner
Anticomplémentaire
À l'inverse, on peut définir comme anticomplémentaire par rapport à un triangle ABC, l'image par homothétie de centre le centre de gravité de ABC et de rapport -2.
Pour un triangle donné, on appelle cercle anticomplémentaire l'anticomplémentaire du cercle circonscrit au triangle, et triangle anticomplémentaire l'anticomplémentaire du triangle de base. Par construction, le triangle anticomplémentaire est donc formé par les parallèles aux côtés du triangle et passant par le troisième sommet, et le cercle anticomplémentaire est le cercle circonscrit à ce triangle.
Références
- Jean-Louis Aymé, « Complémentarité »
- (de) Christian Heinrich von Nagel, Untersuchungen über die wichtigsten zum Dreiecke gehörigen Kreise : eine Abhandlung aus dem Gebiete der reinen Geometrie [« Enquêtes sur les cercles les plus importants appartenant au triangle - un traité de géométrie pure »], Wohler, (présentation en ligne)
- (de) K. G. Reuschle, « Über die Punckte des dreiecks, deren Verbindungsstrecken wom Schwerpunckt gedrittelt », Zeitschrift für Mathematik und Physik, vol. 11, , p. 475-493.
- Emile Vigarié, « Sur les points complémentaires », Mathesis, vol. VII, , p. 6-12
- Adolphe Mineur, Cubiques Anallagmatiques,
Liens externes
- (en) Eric W. Weisstein, « Complement », sur MathWorld
- (en) Eric W. Weisstein, « Anticomplement », sur MathWorld