Clootcransbewijs

La méthode moderne propose de décomposer la force exercée par une boule du fait de la pesanteur terrestre en ses composantes parallèle et verticale au plan incliné (roulement sur un plan incliné). Elle démontre que le dispositif de Stevin est en équilibre et donc n'est animé d'aucun mouvement. Stevin résout le premier ce problème, mais sa solution est fondée sur une considération indirecte et indépendante de la théorie du levier. Il a employé dans sa démonstration, un couple de très puissantes techniques :

• l'imagination et l'expérience pratique de son public, de sorte que le « sens commun » est sollicité ;
• le raisonnement par l'absurde.

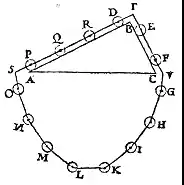
Stevin considère un triangle solide posé sur sa base horizontale en sorte que ses deux côtés forment deux plans inclinés, et il imagine qu'un chapelet formé de plusieurs poids égaux (clootcrans) enfilés à des distances égales ou plutôt une chaîne d'égale grosseur est placée sur les deux côtés de ce triangle, de manière que toute la partie inférieure pende librement au-dessous de sa base comme si elle était attachée aux deux extrémités de cette base[1]. Il suppose que la corde est sans poids et que le mouvement se réalise sans frottement.

• Le nombre de perles sur la pente de gauche est plus faible que sur la pente de droite.

Stevin remarque qu'en supposant que la chaîne puisse glisser librement sur le triangle, elle doit cependant demeurer en repos ; car si elle commençait à glisser d'elle-même dans un sens, elle devrait continuer à glisser toujours puisque la même cause de mouvement subsisterait, la chaîne se trouvant à cause de l'uniformité de ses parties placée toujours de la même manière sur le triangle, d'où résulterait un mouvement perpétuel, ce qui est absurde.

« De cloten sullen uyt haer selven een eeuwich roersel maken, 't welck valsch is » Traduire : « Les boules tourneront par elles-mêmes de manière infinie. Ce qui ne se peut. »

II y a nécessairement équilibre entre toutes les parties de la chaîne; or on peut regarder la portion qui pend au-dessous de la base comme étant déjà en équilibre d'elle-même. Il faut donc que l'effort de tous les poids appuyés sur l'un des côtés contrebalance l'effort des poids appuyés sur l'autre côté ; mais la somme des uns est à la somme des autres dans le même rapport que les longueurs des côtés sur lesquels ils sont appuyés. Donc il faudra toujours un ou plusieurs poids placés sur un plan incliné lorsque le poids total sera proportionnel à la longueur du plan, en supposant la hauteur la même. Mais quand le plan est vertical, la puissance est égale au poids; donc dans tout plan incliné la puissance est au poids comme la hauteur du plan à sa longueur[1].

Stevin suppose que tout le monde comprend qu'une telle machine à mouvement perpétuel ne peut exister. La seule possibilité restante est donc que le postulat de départ est correct : que la charge effective des perles sur les pentes doit être le même rapport que les longueurs des côtés sur lesquels ils sont appuyés[1].

Le théorème de Stevin s'énonce comme suit : « Deux objets sur une pente se tiennent mutuellement en équilibre lorsque leur poids sont dans le même rapport que les longueurs des côtés. »

Le rapport de la puissance au poids sur un plan incliné a été longtemps un problème parmi les mécaniciens modernes. Stévin est le premier à l'avoir énoncé.

Stevin déduit de cette théorie celle de l'équilibre entre trois puissances qui agissent sur un même point, et il trouve que cet équilibre a lieu lorsque les puissances sont parallèles et proportionnelles aux trois côtés d'un triangle rectiligne quelconque.

Mais on doit observer que ce théorème fondamental de la statique quoiqu'il soit communément attribué à Stevin a cependant été démontre par cet auteur que dans le cas où les directions de deux puissances sont entre elles un angle droit. Stevin remarque avec raison qu'un poids appuyé sur un plan incliné et retenu par une puissance parallèle au plan est dans le même cas que s'il était soutenu par deux fils, l'un perpendiculaire et l'autre parallèle au plan et par sa théorie du plan incliné, il trouve que le rapport du poids à la puissance parallèle au plan est comme l'hypoténuse à la base d'un triangle rectangle formé sur le plan par deux droites, l'une verticale et l'autre perpendiculaire au plan. Stevin se contente ensuite d'étendre cette proportion au cas où le fil qui retient le poids sur le plan incliné serait aussi incliné à ce plan en construisant un triangle analogue avec les mêmes lignes, l'une verticale, l'autre perpendiculaire au plan et en prenant la base dans la direction du fil ; mais il faudrait pour cela qu'il eût démontré que la même proportion a lieu dans l'équilibre d'un poids soutenu sur le plan incliné par une puissance oblique au plan, ce qui ne peut pas se déduire de la considération de la chaîne imaginée par Stevin. Il est évident que le théorème de Stevin sur l'équilibre de trois forces parallèles et proportionnelles aux trois côtés d'un triangle quelconque aura pour conséquence le principe de la composition des forces de Pierre Varignon ou plutôt que celui-ci n'est que ce même théorème présenté sous une autre forme[1].

Illustration du Clootcransbewijs.

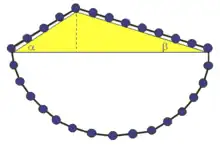
Dans le dessin ci-joint il y a 4 perles sur la pente de gauche, et 8 sur la pente de droite. Les composantes de la force le long de la pente égalent la force de gravité × sin(angle d'inclinaison), en d'autres termes:

${\displaystyle F_{//}=m\,g\,\sin({\textrm {pente}})}$

Le sin(α) doit être 2 fois aussi grand que sin(β), et cela n'est vrai que si la pente de gauche est aussi longue que la moitié de la pente de droite. Les deux forces le long des pentes à gauche et à droite à partir du haut sont en effet en équilibre:

${\displaystyle \sin \alpha =2\,\sin \beta }$

${\displaystyle F_{//,{\textrm {gauche}}}=4\,m\,g\,\sin \alpha =F_{//,{\textrm {droite}}}=8\,m\,g\,\sin \beta }$

avec:

• F_// = force (en newton) le long de la pente face
• m = masse d'une bille (en kg)
• g = accélération due à la gravité (en m.s^-2)

• A Visual Riddle (The Epitaph of Stevinus)

• (nl) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en néerlandais intitulé « Clootcransbewijs » (voir la liste des auteurs).

• Itard Jean. The Principal Works of Simon Stevin, Edited and annotated by a Committee of Dutch scientists. In: Revue d'histoire des sciences et de leurs applications, tome 9, n^o 1, 1956. p. 95-96. Lire en ligne