Chiffre VIC
Le chiffre VIC fut un chiffre utilisé au début des années 1950 par l'espion soviétique Reino Häyhänen (nom de code VICTOR), basé à l'époque à New York. Le VIC appartient à la famille des chiffres nihilistes et consiste en une combinaison complexe de substitutions et de transpositions.
Histoire
Le premier texte chiffré en VIC fut découvert par hasard par James Bozart en 1953. Livreur de journaux à l'époque, il fit tomber plusieurs pièces de monnaie dans un escalier et constata qu'une pièce de 5 cents était creuse et contenait un microfilm carré. Ce chiffre a résisté à tous les efforts de pénétration de la NSA[1]. Ce fut Häyhänen lui-même qui en expliqua le principe au moment de sa défection, en 1957, à l'ambassade américaine à Paris.
Présentation
Le chiffre VIC se fait en douze étapes et nécessite pour l'utilisateur de mémoriser plusieurs données[1]:
- les huit lettres les plus fréquentes dans la langue concernée (publique) ;
- une suite de 6 chiffres (secrète) ;
- un vecteur d'initialisation de 5 chiffres (public) ;
- une suite de 20 lettres (secrète) ;
- un code personnel entre 1 et 16 (secret).
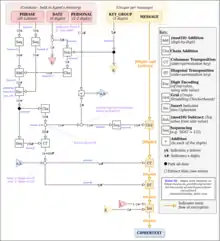
Fonctionnement détaillé
Note: Dans les chapitres ci-dessous, les étapes sont nommées [Line-X] afin de suivre la notation de la description qui en est faite dans les archives de la CIA[2]. Il n'y a pas de [Line-I] et [Line-O], sans doute pour éviter l’ambiguité avec 1 et zéro.
exemple pour les étapes ci-dessous
| Numéro de l'agent | 6 | |
| Date | 13/09/1959 | Alunissage de Luna-2 |
| Phrase | 'Twas the night before Christmas' | 'A visit from St. Nicholas' - poème par Clement Clarke Moore |
| Keygroup | 72401 | Nombre aléatoire de 5 digits |
[Line-A]
Génération d'une clef aléatoire de 5 chiffres (Keygroup)
Keygroup: 72401
[Line-B]
Écrit les 5 premiers chiffres de la date sans les zéro (Date)
Date: 13919
[Line-C]
Soustrait [Line-B] de [Line-A] par arithmétique modulaire (chiffre par chiffre, pas de retenue entre colonnes voisines)
69592: 7-1=6, 2-3=9, 4-9=5, ...
[Line-D]
Choisit une phrase secrète et écrit les 20 première lettres (Phrase)
TWASTHENIG HTBEFORECH
[Line-E.1&2]
séquençage (voir ci-dessous "opérations") du premier et le second groupe de 10 caractères de [Line-D], ce qui donne [Line-E.1] et [Line-E.2] respectivement
[Line-E]: 8017942653 6013589427
[Line-F.1]
Prend les 5 premiers caractères de [Line-C], puis applique l'addition de chaine (voir ci-dessous "opérations") pour créer 5 chiffres supplémentaires.
[Line-F.1]: 6959254417
[Line-F.2]
on écrit la séquence de chiffres '1234567890' (sous [Line-E.2]) comme support pour encoder [Line-H]
[Line-F.2]: 1234567890
[Line-G]
Additionner [Line-E.1] et [Line-F.1] (colonne par colonne, sans retenue comme pour [Line-C])
[Line-G]: 4966196060
[Line-H]
encoder (voir ci-dessous)les chiffres de [Line-G] en utilisant [Line-E.2] comme clef
[Line-H]: 3288628787
[Line-J]
Séquençage de [Line-H]
[Line-J]: 3178429506
[Lines-K,L,M,N,P]
Ce sont des lignes de 10 chiffres crées par addition de [Line-H]. Les derniers chiffres non-égaux sont ajoutés au numéro personnel de l'agent pour déterminer la longueur de la clef des 2 transpositions. (Lines K-à-P sont en effet une génération pseudo-aléatoire basée sur la clef, utilisée par les étapes suivantes du chiffrage)
[Line-K]: 5064805552 [Line-L]: 5602850077 [Line-M]: 1620350748 [Line-N]: 7823857125 [Line-P]: 5051328370
[Line-Q]
Le premier chiffre 'a' extrait des lignes [Lines-K,L,M,N,P] transposées par [Line-J]. (Avec 'a', première valeur résultant de l'addition du dernier chiffre non-égal de [Line-P] avec le numéro de l'agent). Utilisé comme clef de la transposition en colonne.
[Line-R]
Le second chiffre 'b' est extrait (après le chiffre 'a') des lignes [Lines-K,L,M,N,P] transposées par [Line-J]. (Avec 'b', seconde valeur résultant de l'addition du dernier chiffre non-égal de [Line-P] avec le numéro de l'agent). Utilisé comme clef de la transposition en diagonale.
[Line-S]
Le séquencement de [Line-P], utilisé comme clef de l'échiquier à diffusion.
Séquençage
Le séquençage est ici la numérotation séquentielle de 1 à 10 (0 représente 10) des éléments d'un groupe triés dans l'ordre. En cas de répétition, on donne le premier numéro à celui de gauche. Exemples:
- le mot 'Octopus'. Lettres dans l'ordre: COOPSTU, numérotées: 1234567. On remplace les lettres par ces nombres: Octopus = 2163475
- Le nombre '90210', chiffres dans l'ordre croissant (0=10): 12900, donne: 123456. On remplace les chiffres par leur ordre: 34215
encodage des digits
L'encodage remplace chaque nombre (ex: [Line-G]) par la clef (ex: [Line-E.2]), digit par digit. On encode chaque digit par le digit au-dessus dans la table:
| Clef | (Line E.2) | 6 | 0 | 1 | 3 | 5 | 8 | 9 | 4 | 2 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aide | (Line F.2) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
Par exemple le nombre '90210' serait encodé ainsi; .
résultat: '27067'.
Échiquier à diffusion
Une fois la clef générée, la première étape du chiffrage réel est de convertir le message en une série de digits. C'est fait avec un échiquier à diffusion. La clef est basée sur la [Line-S] et comporte les 10 digits 0 à 9. En deuxième ligne, on met normalement les lettres les plus courantes de la langue. Ici 'AT ONE SIR' pour l'anglais. On complète les autres lignes avec les lettres restantes, puis . et /. Les lignes suivantes sont numérotées en utilisant les 2 chiffres correpondant à des cases vides de la première ligne.
| 5 | 9 | 6 | 1 | 3 | 2 | 8 | 4 | 7 | 0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | T | O | N | E | S | I | R | |||
| 6 | B | C | D | F | G | H | J | K | L | M |
| 8 | P | Q | U | V | W | X | Y | Z | . | / |
Exemple:
MESSAGE: 'Attack at dawn. By dawn I mean 0500. Not 0915 like you did last time.' 59956 96459 66583 38765 88665 83376 02538 00005 55000 00080 87319 80000 99911 15558 06776 42881 86667 66675 49976 0287-
Notez que les lettres de la première ligne du tableau utilisent un seul digit. A=5, T=9, C=69, K=64
Références
- Pascal Boyer, Petit compagnon des nombres et de leurs applications, Calvage et Mounet, , 648 p. (ISBN 978-2-916352-75-6), VI. Cryptographie, chap. 1.5 (« Enigma et VIC : deux codes du XXesiècle »), p. 514-519.
- (en) David Kahn, Number One From Moscow, CIA, , 16 p. (lire en ligne)
