Brique d'Euler

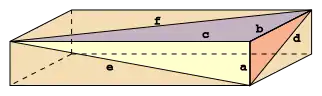
Une brique d'Euler est un parallélépipède rectangle dont les arêtes et les diagonales des faces ont des longueurs entières. Appelée aussi brique de Pythagore [1] - [2], elle porte le nom du mathématicien Leonhard Euler qui en a déterminé des familles infinies en 1771[3] - [4].

Brique d'Euler avec côtés a,b,c et diagonales des faces d,e,f.

Formulation arithmétique

Les dimensions d'une brique d'Euler correspondent à une solution en nombres entiers strictement positifs du système d'équations diophantiennes :

{\begin{cases}a^{2}+b^{2}=d^{2}\\a^{2}+c^{2}=e^{2}\\b^{2}+c^{2}=f^{2}\end{cases}}

où $a, b, c$ sont les longueurs des arêtes de la brique et $d, e, f$ les longueurs des diagonales des faces.

Si $(a, b, c)$ est une solution, alors $(ka, kb, kc)$ est aussi une solution pour tout entier strictement positifs $k$ . On désigne donc par brique primitive une brique où $a, b, c$ sont premiers entre eux.

Fac-similé du texte de Paul Halcke, demandant de trouver trois carrés tels que si on en additionne deux, viennent alors trois carrés : 44²=1 936, 240²=57 600, 117²=13 689.

Exemples

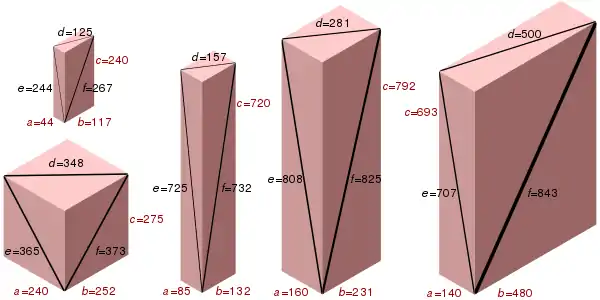
La brique d'Euler de plus petit volume $abc$ a été découverte en 1719, non par Euler, mais par Paul Halcke (de) [5] ; elle a pour côtés $(a, b, c) = (44, 117, 240)$ et pour diagonales des faces ( $d, e, f$ ) = (125, 244, 267).

Sont représentées ci-dessous les cinq briques d'Euler primitives dont les dimensions sont inférieures à mille.

Si l'on classe les briques d'Euler primitives par ordre croissant de la plus grande arête, les listes des longueurs des plus grandes arêtes, des arêtes intermédiaires, et des plus petites arêtes sont données par les suites de l'OEIS : A031173, A031174 A031175.

Propriétés

Si $(a, b, c)$ sont les dimensions d'une brique d'Euler, alors la brique de dimensions $(ab, ac, bc)$ est également une brique d'Euler, de diagonales $(af, be, cd)$ .

Démonstration

Comme $(a, b, c)$ forme une brique d'Euler, il existe trois entiers $d, e, f$ tels que

{\begin{cases}a^{2}+b^{2}=d^{2}\\a^{2}+c^{2}=e^{2}\\b^{2}+c^{2}=f^{2}\end{cases}}

En multipliant la première ligne par $c 2$ , la deuxième par $b 2$ et la troisième par $a 2$ , on obtient

{\begin{cases}(ac)^{2}+(bc)^{2}=(dc)^{2}\\(ab)^{2}+(cb)^{2}=(eb)^{2}\\(ba)^{2}+(ca)^{2}=(fa)^{2}\end{cases}}

où $dc, eb, fa$ sont des entiers.

Ceci montre que le triplet $(ab, ac, bc)$ constitue une brique d'Euler.

Si la brique de départ est primitive, et si on divise les termes de $(ab, ac, bc)$ par leur PGCD, on obtient une brique primitive dite conjuguée de celle de départ (la conjuguée de la conjuguée redonnant la brique de départ) [6]. Par exemple, les deux grandes briques de dimensions (160, 231, 792) et (140, 480, 693) du dessin ci-dessus sont conjuguées.

Parmi les nombres $a, b, c$ , l'un est multiple de 4, un autre, multiple de 16, l'un est multiple de 3 et un autre multiple de 9, l'un est multiple de 5, et l'un est multiple de 11. Le volume $abc$ de la brique est donc divisible par $64\times 27\times 5\times 11=95\,040$ [2] - [6]. Par exemple, le volume de la plus petite brique d'Euler est $1\,235\,520=13\times 95\,040$ .

Familles infinies

Une famille infinie de briques d'Euler a été trouvée par Nicholas Sounderson en 1740 dans son ouvrage "The Elements of Algebra, in Ten Books" [4] - [6], donc antérieurement à la publication d'Euler, qui a redécouvert cette famille [3].

Soit $(u,v,w)$ un triplet pythagoricien (vérifiant donc $u^{2}+v^{2}=w^{2}$ ) alors :

$a=u|4v^{2}-w^{2}|,\quad b=v|4u^{2}-w^{2}|,\quad c=4uvw$ sont les arêtes d'une brique d'Euler,

et $d=w^{3},\quad e=u(4v^{2}+w^{2}),\quad f=v(4u^{2}+w^{2})$ en sont les diagonales.

Par exemple, le triplet pythagoricien minimal (3, 4, 5) fournit la brique minimale (44, 117, 240).

Malheureusement cette famille ne donne pas toutes les briques d'Euler (remarquer que $d$ est un cube) comme par exemple la brique d'Euler d'arêtes ( $a, b, c$ ) = (240, 252, 275) et de diagonales ( $d, e, f$ ) = (348, 365, 373) .

Il existe d'autres familles infinies, mais on n'a pas trouvé de famille recouvrant tous les cas possibles, comme pour les triplets pythagoriciens [4].

Brique d'Euler parfaite

Une brique d’Euler est dite parfaite si la diagonale principale qui joint deux sommets opposés a également une longueur entière. Aucune brique de Sounderson ci-dessus n'est parfaite, ni aucune de leurs conjuguées [7], et aucun exemple de brique parfaite n’est connu à ce jour, mais on n'a pas démontré non plus leur inexistence.

Notes et références

François Le Lionnais, Les nombres remarquables, Paris, Hermann, 1983, p. 45
M. D. Indjoudjian, « Récréations scientifiques », La Jaune et la Rouge,‎ mars 1998, p. 39 et 42-43 (lire en ligne)
(de) Leonhard Euler, Vollständige Anleitung zur Algebra, II : Fragmenta commentationis cuiusdam maioris, de invenienda relatione enter latera triangulorum, quorum area rationaliter exprimi possit, St. Petersburg, Kayserliche Akademie der Wissenschaften, 1771 (lire en ligne)
Daniel Lignon, Dictionnaire de (presque) tous les nombres entiers, Paris, Ellipses, 2012, p. 574-575
Visions of Infinity: The Great Mathematical Problems By Ian Stewart, Chapter 17
Francis Casiro, « Les briques d'Euler », Hors Série Tangente n°29, Leonhard Euler, Un génie des Lumières,‎ 2007
Jean Lagrange, « Sur le dérivé du cuboïde eulérien », Canad. Math. Bull. Vol. 22 (2),‎ 1979 (lire en ligne)

Articles connexes

Cet article est issu de wikipedia. Text licence: CC BY-SA 4.0, Des conditions supplémentaires peuvent s’appliquer aux fichiers multimédias.